Decide whether the equation is a trigonometric identity explain your reasoning cos^2x(1tan^2x)=1 secxtanx(1sin^2x)=sinx cos^2(2x)sin^2=0 ** cos^2x(1tan^2x)=1 cos^2xsin^2x/cos^2x=1 cos^2xsin^2x=1 left side = right side, therefore, equation is an identity secxtanx(1sin^2x)=sinx (1/cosx*sinx/cosx)(11cos^2x (sinx/cos^2x)(cos^2x)=sinx2 x I started this by making sec 1/cos and using the double angle identity for that and it didn't work at all in any way ever Not sure why I can't do that, but something was wrong Anyways I looked at the solutions manual and they magic out 1 tan x tan 2 x = 1 tanThe Pythagorean Identities Cool Math has free online cool math lessons, cool math games and fun math activities Really clear math lessons (prealgebra, algebra, precalculus), cool math games, online graphing calculators, geometry art, fractals, polyhedra, parents and teachers areas too

Chapter 7 Trigonometric Identities And Equations Jami Wang
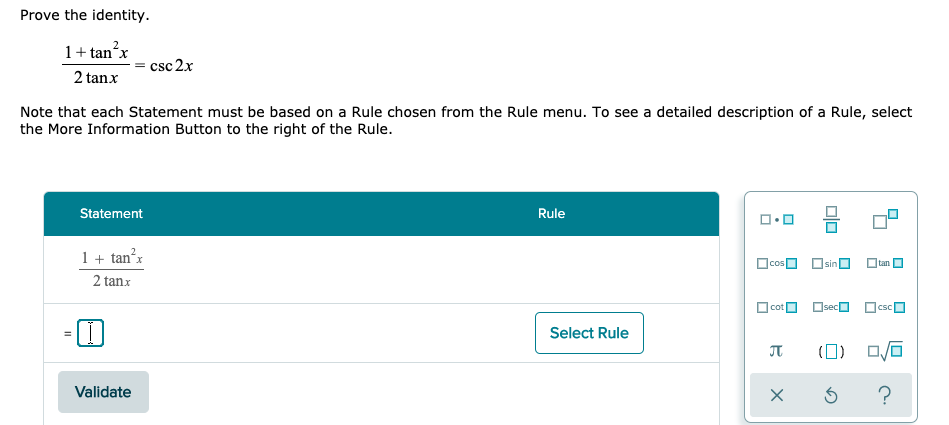
Prove the identity 1+tan^2x/2tanx=csc2x
Prove the identity 1+tan^2x/2tanx=csc2x-1 1 Because the two sides have been shown to be equivalent, the equation is an identity cos2(x)(1tan2(x)) = 1 cos 2 (x) (1 tan 2 (x)) = 1 is an identity1 cos ( x) − cos ( x) 1 sin ( x) = tan ( x) Go!




2sinxcosx Identity Gamers Smart
Use identities to simplify the expression 1 tan 2x 2 COS X 1 2 tan x 10 2 COS X Verify that the trigonometric equation is an identity, (1 cos ?a)(1 cos?a) = 2 sinļa sina Which of the following statements establishes the identity?Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Question Show all steps necessary to verify the trigonometric identity 1tan^2x = csc^2x tan^2x Answer by jsmallt9(3758) (Show Source) You can put this solution on YOUR website!
Verify the Identity 12cos (x)^2= (tan (x)^21)/ (tan (x)^21) Start on the right side Apply pythagorean identity Apply Pythagorean identity in reverse Convert to sines and cosines Tap for more steps Apply the reciprocal identity to sec ( x) sec ( x) Apply the reciprocal identitySolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreMath\sin^2x\cos^2x=1/math math\implies\dfrac{\sin^2x}{\cos^2x}\dfrac{\cos^2x}{\cos^2x}=\dfrac{1}{\cos^2x}/math math\implies\left(\dfrac{\sin x}{\cos x
Because the two sides have been shown to be equivalent, the equation is an identity (sec(x)1)(sec(x)−1) = tan2 (x) (sec (x) 1) (sec (x) 1) = tan 2 (x) is an identityShow all steps necessary to verify the trigonometric identity (1tan^2x)/tan^2x=csc^2x 2 See answers 1tan^2(x) = 1 (sin2x)/(cos2x) = cos2x sin2x/cos2x = cos 2x/cos2x is a posibly 'simplified' version in that it has been boiled down to only cosines




F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic
Some trigonometric identities follow immediately from this de nition, in particular, since the unit circle is all the points in plane with xand ycoordinates satisfying x2 y2 = 1, we have cos2 sin2 = 1 Other trignometric identities re ect a much less obvious property of the cosine and sine functions, their behavior under addition of angles Middle School answer answered PLEASE HELP!!!Sin^2x cos^2x = 1 Pythagorean Identity 1 tan^2x 1 = sec^2x pythagorean identity 2 cot^2x 1 = csc^2x Pythagorean identity 3 tanx sinx/cosx secx




Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com




Tan2x ただの悪魔の画像
Get an answer for 'verify (1 tan^2x)/(tan^2x) = csc^2x' and find homework help for other Math questions at eNotes Verify the identity `1/(tan^2x) 1/(cot^2x) = csc^2x sec^2x` 22tanx/1tan^2x YOU MIGHT ALSO LIKE Reciprocal, Quotient, and Pythagorean Identities 8 terms jessgac00 Trigonometric Identities some 35 terms baaskat000 trigometric identities Start studying Trig Identities Learn vocabulary, terms, and more with flashcards, games, and other study tools Home Subjects Browse Languages EnglishFirst I join fractions (Easy) then I "express" tans in




What Is The Formula Of Tan2x Quora




Answered 1 8 Verify Each Identity 1 Tan 0 Bartleby
1tan^2x=sec^2x Change to sines and cosines then simplify 1tan^2x=1(sin^2x)/cos^2x =(cos^2xsin^2x)/cos^2x but cos^2xsin^2x=1 we have1tan^2x=1/cos^2x=sec^2x Trigonometry Science The correct identities are 1 tan^2x = sec^2x 1 cot^2x = csc^2x sin^2x cos^2x = 1 which correspond to B and D thank you!!!Tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx Integral of the function \frac {\cos ^2 x} {1\tan x}
x-1=sec(squared)x.jpg)



10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com




Simplify This Trig Function 1 Tan 2x Csc 2x Youtube
As the length of the perpendicular and base is given;Free math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantlyFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor




Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi



How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora
Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify Statistics Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal DistributionVerify the identity {eq}1 \tan^2x = \frac{\cos2x}{\cos^2x} {/eq} Identity An identity is an equation that holds true for any given variable value We have many commonly used trigonometricTan(2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin(2x) to cos(2x) sin(2 x) = 2 sin(x) cos(x) cos(2 x) = (cos(x))^2 – (sin(x))^2 =



1




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
B) (tanx 1)(tanx1)/1 tan^2(x) = (sinx/cosx 1)(sinx/cosx 1) / 1/cosx then again I'm stuck!1 sin 2x = 1 sin 2x (Pythagorean identity) Therefore, 1 sin 2x = 1 sin 2x, is verifiable HalfAngle Identities The alternative form of doubleangle identities are the halfangle identities Sine • To achieve the identity for sine, we start by using a doubleangle identityFirst of all, please do not try to use fraction bars when you post Most of the time they look so bad they are hard to understand




2sinxcosx Identity Gamers Smart



App Shoreline Edu Fmarchetti M142 Materials Identities Pdf
Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4 cot x = 1/tan x equation 5 sin 2 x cos 2 x = 1 equation 6 tan 2 x 1 = sec 2 x equation 7 1 cot 2 x = csc 2 x equation 8 cos (x y) = cos x cos y sin x sin y equation 9 sin (x y) = sin x cos y cos x sin y equation 10 cos (x) = cos x equation 11How do you prove ##(1 tan^2x)/(1tan^2x) = 1/(cos^2x sin^2x)##? Prove $$\frac{2\tan x}{1\tan^2x}\frac1{2\cos^2x1} = \frac{\cos x\sin x}{\cos x\sin x}$$ I know how to solve it, yet I can't!




Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity




How Do You Prove Tan 2x Secx 1 1 Secx Socratic
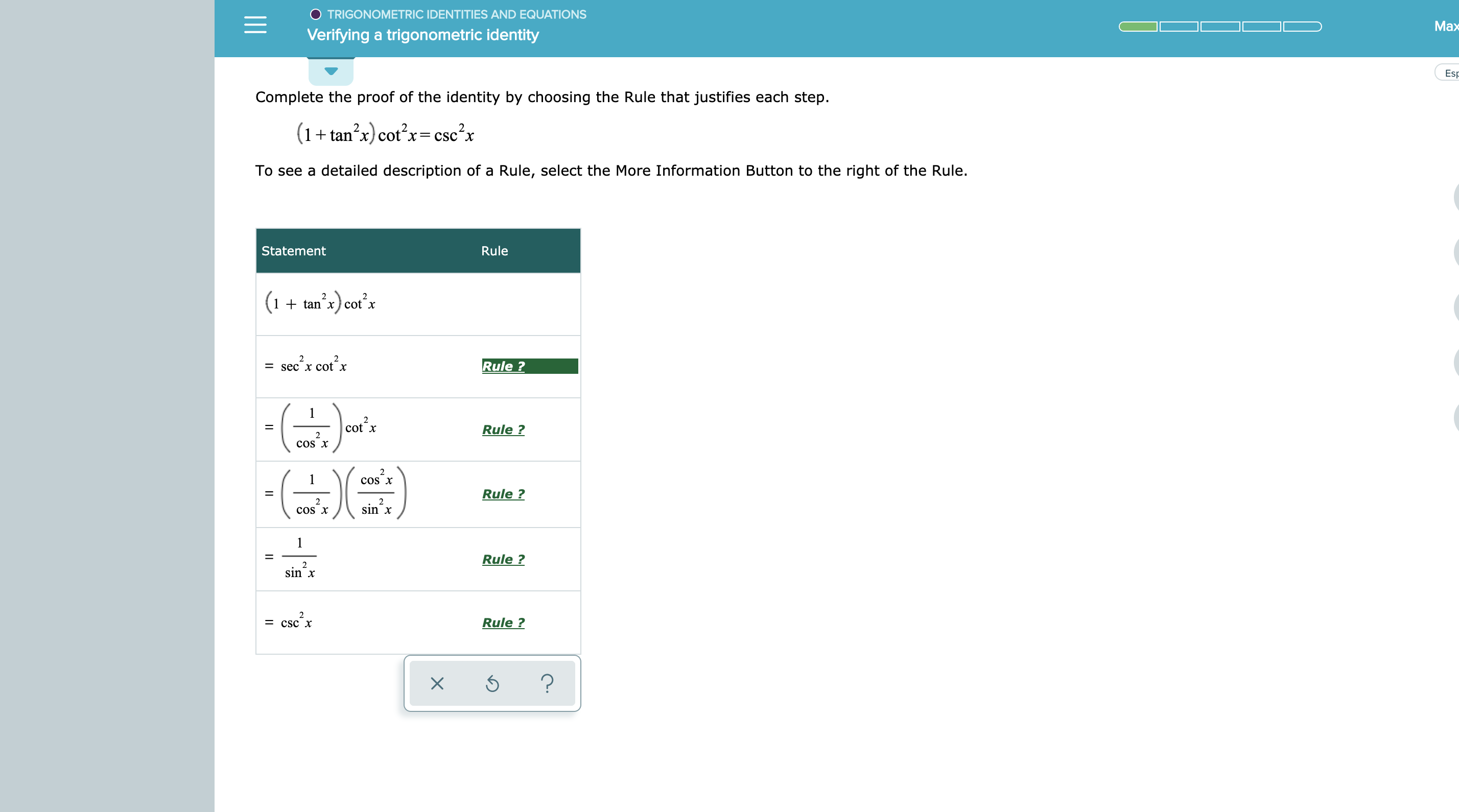
RH S = cos2x = cos(x x) = cosx ⋅ cosx − sinx ⋅ sinx = cos2x − sin2x = cos2x −sin2x cos2x sin2x = cos2x cos2x − sin2x cos2x cos2x cos2x sin2x cos2x = 1 − tan2x 1 tan2x = LH S Answer linkIn this video I go over the proof of another trigonometry identity and this time prove the identity 1 cot^2(x) = csc^2(x) The proof for this is similar tQuestion I need to prove the identity (1tan^2x)cot^2x=csc^2x Found 2 solutions by Alan3354, Regrnoth Answer by Alan3354() (Show Source) You can put this solution on YOUR website!




Tan 2x Formula What Is Tan 2x Formula Examples



Derivatives Of Trigonometric Functions
A follow up proof to accompany sin^2 cos^2 =1 Another identity that is used quite a bit, especially in calculus involving trigonometric functionsNow use the identity to get the denominator in terms of cosine Multiply the first fraction by the reciprocal of the second fraction Get tangent in terms of sine and cosine 1 or (tan^2(x)1)(tan^2x1) then i'm stuck!Flightbath flightbath Answer Option B and D are correct Stepbystep explanation Option A is incorrect because the correct identity we have is




Is There Any Other Way To Establish This Trig Identity Frac Sec X 1 Tan X Frac Sin X 1 Cos X Mathematics Stack Exchange




Answered Verify The Identity 2 Tan X 1 Bartleby
Establish the identity (1 sin^2(x))(1 tan^2(x)) = 1Sin^2x (1cot^2x)=1 distributing the sin^2x sin^2x sin^2xcot^2x = 1 substitute identity of "cot^2x" = cos^2x/sin^2x sin^2x sin^2x (cos^2x/sin^2x) = 1Algebra > Trigonometrybasics> SOLUTION Complete the sentence so the result is an identity Let x be any real number _sin^2x=1 1_=sin^2x _1=tan^2x Log On
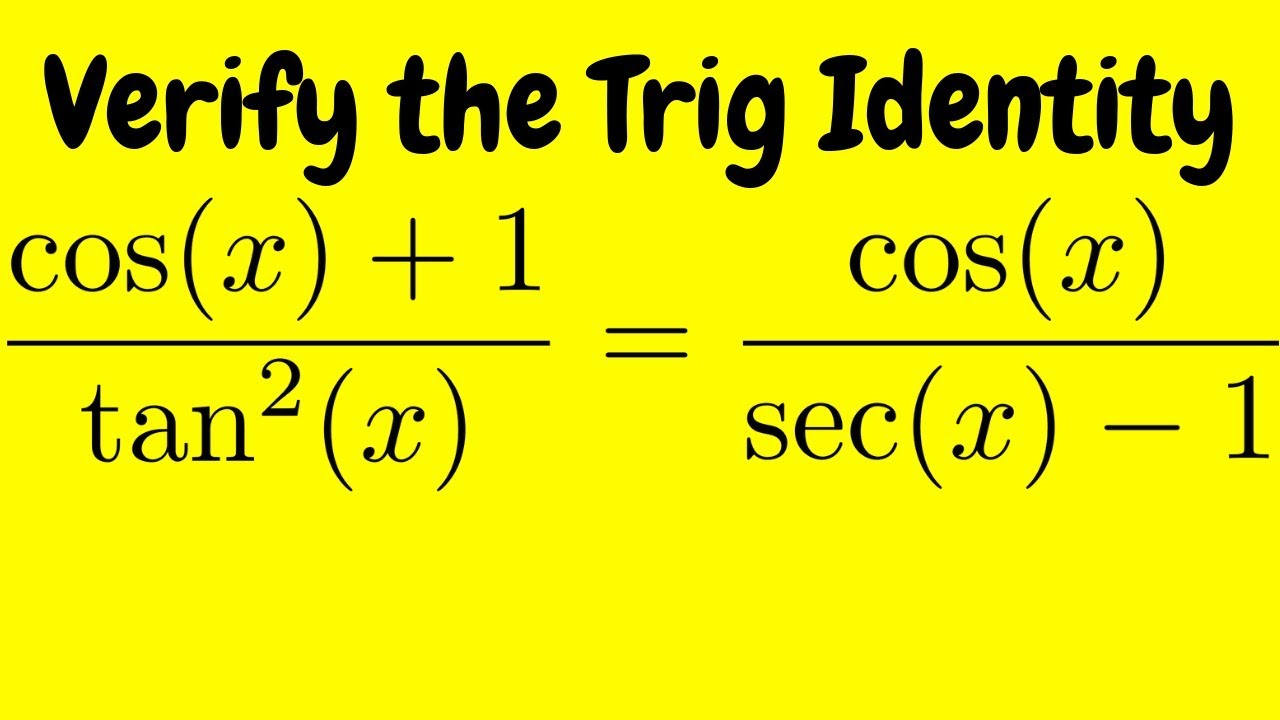



Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube




Proof Tan 2 1 Sec 2 Youtube
Trigonometric Identities Solver \square! It is 1tan^2x = sec^2x So there isn't a really simple way to get 1tan^2x Trig Trigonometry Identities Triangles Mathematics Math Word Problem Tangent Trigonometric Identities Trigonometric Functions Cosine Sine RELATEDSUMMER 07 PAPER 1 QUESTION 3




2sinxcosx Trig Identity Gamers Smart




Find The General Solution Sec22x 1 Tan 2x Maths Trigonometric Functions Meritnation Com
It can be concluded that, tan A = 3/4 Now, using the trigonometric identity 1tan2 a = sec2 a sec2 A = 1 (3/4)2 sec 2 A = 25/16 sec A = ±5/4 Since, the ratio of lengths is positive, we can neglect sec A = 5/4 Therefore, sec A = 5/4Substitute the trigonometric identity `tan^2(x) = sec^2(x)1` Note This is the same as `1 tan^2(x) = sec^2(x)` `(tan^2(x))/(1tan^2(x)) = (sec^2(x)1)/(sec^2(x))`Introduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula



1 Point If Tan X 1 3 Cosx 0 Then Sin 2x Cos 2x Homeworklib
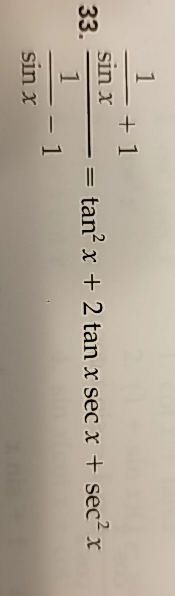



Verify The Identity Math Frac Frac 1 Sin X 1 Frac 1 Sin X 1 Tan 2x 2 Tan X Sec X Sec 2x Math Homework Help And Answers Slader
Proving Trigonometric Identities Calculator Get detailed solutions to your math problems with our Proving Trigonometric Identities stepbystep calculator Practice your math skills and learn step by step with our math solver Check out all of our online calculators here!Now apply identity tan (ab)= (tan a tan b)/ (1tan atan b) tan2x can be solved by this method then by doing Tan (xx) and you will get tan2x=2tanx/ (1 tanxsquare) Tan3x=3tanx cube of tanx/1–3*square if tanx 69K views · View upvotes Sponsored by Best Gadget AdviceThese identities are useful whenever expressions involving trigonometric functions need to be simplified An important application is the integration of nontrigonometric functions a common technique involves first using the substitution rule with a trigonometric function, and then simplifying the resulting integral with a trigonometric identity




Chapter 7 Trigonometric Identities And Equations Jami Wang




Tangent Half Angle Formula Wikipedia
Left hand side identity = (1Tan^2x)/Csc^2x = (1Tan^2x)/(1/Sin^2x) = Sin^2x(1Tan^2x) = (1Cos^2x)(1Tan^2x) = 1Tan^2xCos^2xCos^2xTan^2x =Transcribed Image Textfrom this Question Complete the proof of the identity by choosing the Rule that justifies each step cosx (1 tan 2x)secr To see a detailed description of a Rule in the Rule menu, select the corresponding question mark Statement Rule cosxtanx cosx (secr Rule ?(1tan^2x)/(1tan^2(x)) 1 = 2cos^2(x)



Prove That Cos2x Cos 2x Sin 2x 2cos 2x 1 1 2sin 2x 1 Tan 2x 1 Tan 2x Sarthaks Econnect Largest Online Education Community




Ch 7 Trigonometric Identities And Equations Ppt Video Online Download
1 cos?a) (1 cos?a) cot?a( csc?a1) cot?a ( cot'u11) 2 sin'a sin *x OBProve the identity Answer by nerdybill (7384) ( Show Source ) You can put this solution on YOUR website!
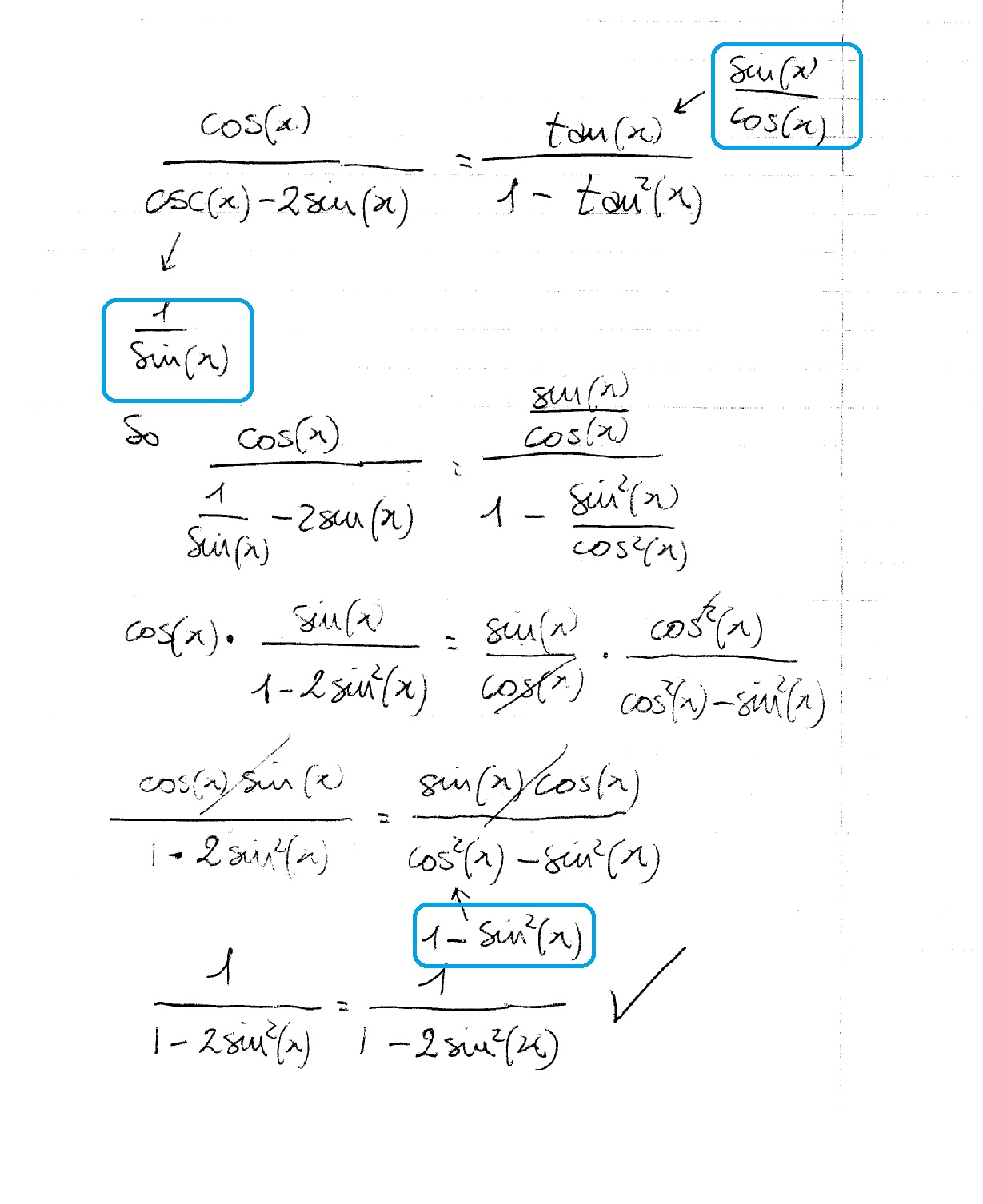



How Do You Prove Cosx Cscx 2sinx Tanx 1 Tan 2x Socratic



Www Birmingham K12 Mi Us Cms Lib Mi Centricity Domain 976 Chapter 5 Pdf




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube



3




W H E R E I S T A N 1 Zonealarm Results




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube




Solve Tan 2 X 1 0 Yahoo Answers Noha Matthieu Lire Un Livre




Establish The Identity 1 Sin 2 X 1 Tan 2 X 1 Youtube




Trig Identities And Formulas Pre Calculus Quiz Quizizz




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




5 1 Fundamental Trig Identities Reciprocal Identities Sin




Verify The Identity 4 2 Tan X Secx2tan X 1 Which Chegg Com




5 2 Verify The Following Trigonometric Identities A Chegg Com



Solution Show All Steps Necessary To Verify The Trigonometric Identity 1 Tan 2x Csc 2x Tan 2x




Prove The Identity 1 Tan 2x 1 Tan 2x 1 2sin 2x In Urdu Hindi Youtube
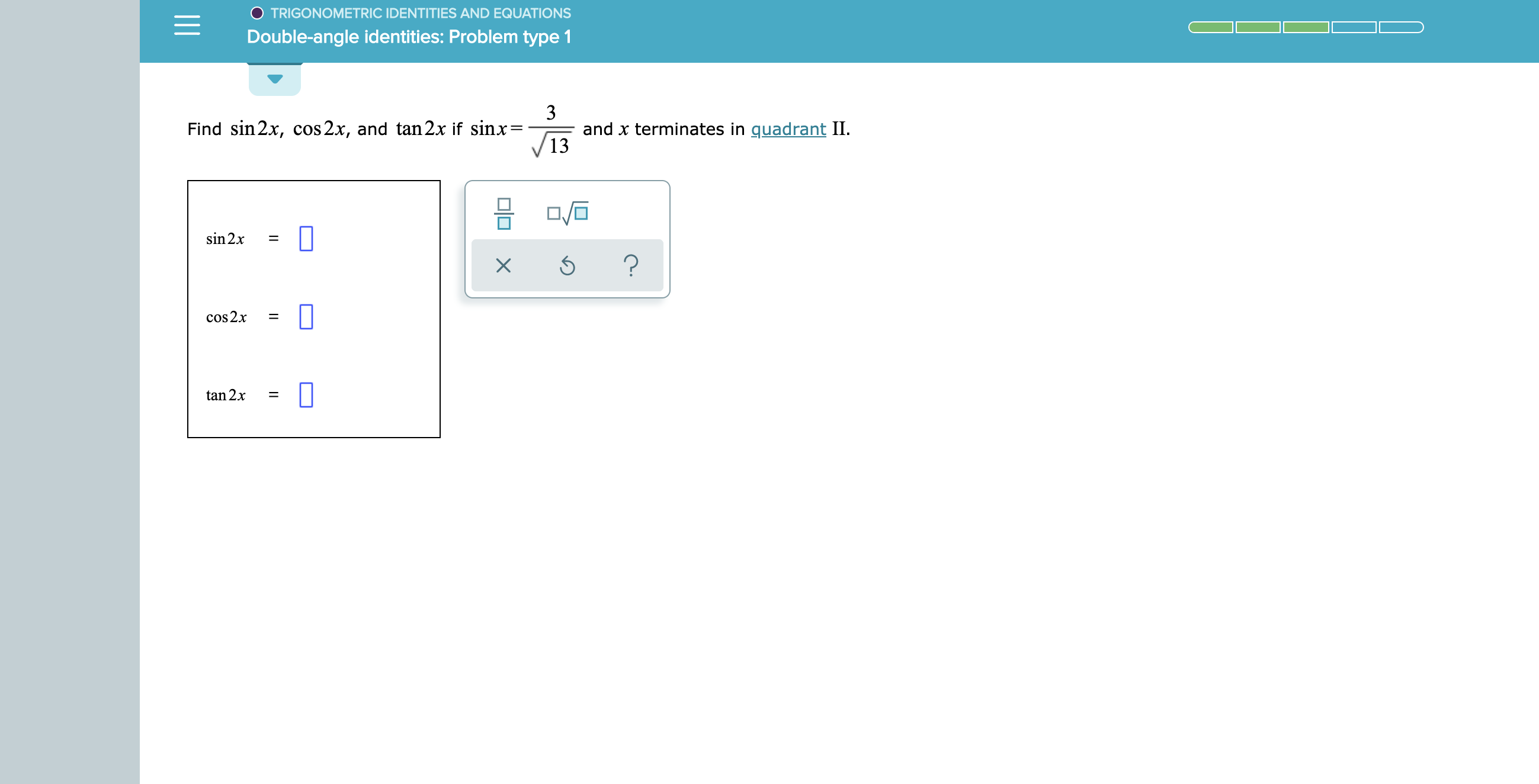



Answered Trigonometric Identities And Equations Bartleby
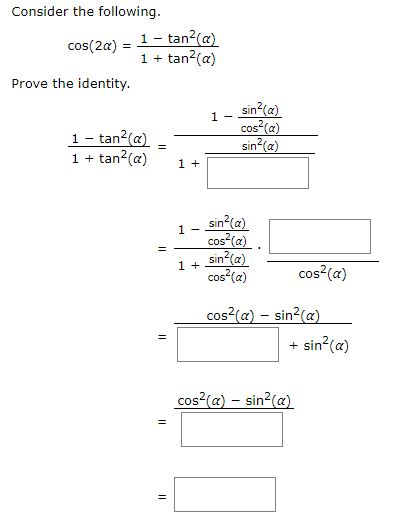



Prove The Identity 2 Tan X Sin 2x 1 Tan2x Write Chegg Com



Tan2x ただの悪魔の画像




Ch Ppt Download




Sec 1 1 Tan 2x 1 Tan 2 X




The Expression 1 Tan X Tan 2 X 1 Cot X Cot 2 X Has The




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube




Ashley Avery Free Books Catalog



View Question For Questions 1 5 Decide Whether The Equation Is A Trigonometric Identity Explain Your Reasoning




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




Answered Prove The Following Identity 1 Tan X Bartleby




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic



A Trig Identity



Tan2x ただの悪魔の画像




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube



What Is The Formula Of Tan2x Quora




Using Trigonometric Identities Video Khan Academy



1




Solved Prove The Identity Cot 2x 1 Tan 2x 2 Tan X Pro Chegg Com
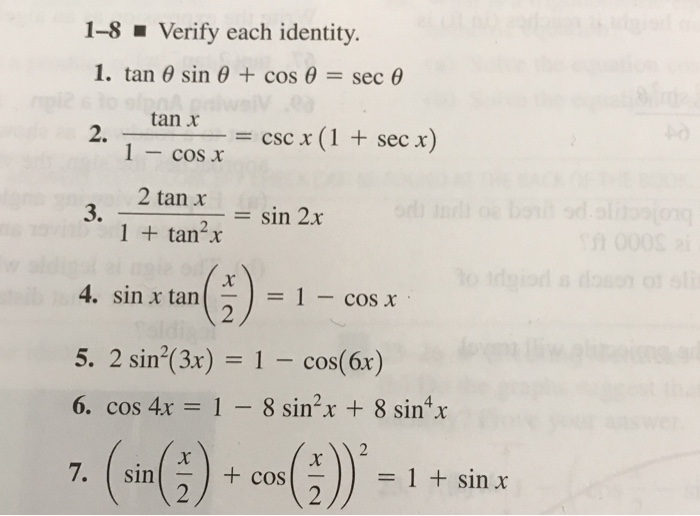



1 8 Verify Each Identity Sec 8 1 Tan 8 Sin 8 Chegg Com




5 1 Fundamental Trig Identities Reciprocal Identities Sin



7 Proving Ids Trig Functions Identities




Chapter 7 Trigonometric Identities And Equations Ppt Download




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




Trigonometry Reciprocal Identities Expii



How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora




Double Angle Identities Solutions Examples Videos Worksheets Games Activities




Verify The Identity 2 Tan X Sin 2x 1 Tan2 X 2 Chegg Com



Prove Sin2x 2tanx 1 Tan 2x Socratic



How To Prove Math Dfrac Sqrt 1 Cos 2x 1 Cos 2x Tan X Math Quora



1




Integrate Sec 2x Method 1
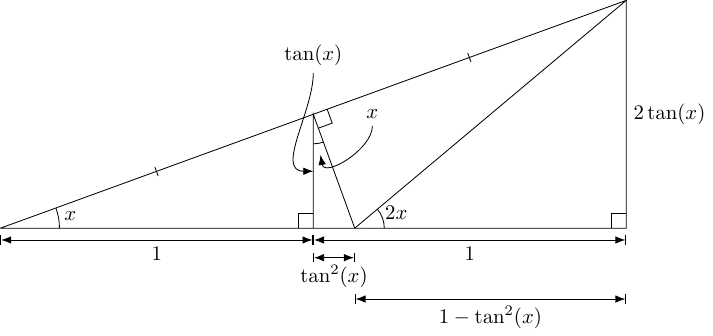



Triangles And Identities




Prove The Identity 1 Tan X Tan Y Cos X Y Chegg Com




3 Simplifying Trig Expression 1 Tan 2x Youtube
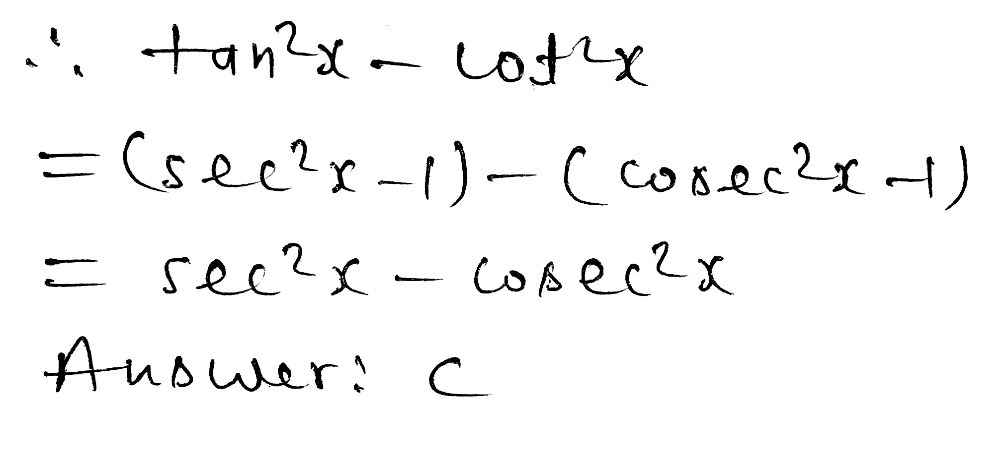



Use Trig Identities To Simplify Tan 2x Cot 2x A Gauthmath



What Is The Formula Of Tan2x Quora




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube



Answered Trigonometric Identities And Equations Bartleby




Half Angle Identities



10 4 Integration Of Powers Of Trigonometric Functions
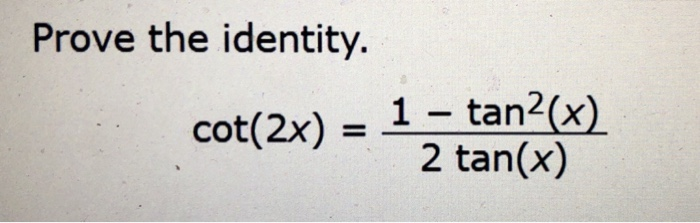



Prove The Identity Cot 2x 1 Tan2 X 2 Tan X Chegg Com



Quandaries Queries Math Central




Weierstrass Substitution Wikipedia




8 Prove That Cos2x 1 Tan 2x 1 Tan 2x Brainly In




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic




Trig Identity Sec2x Minus Tan2x T10 Youtube



True Or False The Equation Sec 2 X 1 Tan 2 X Is An Identity Brainly Com



Prove The Identity 1 Tan X 2 Tanx Csc 2x Note Chegg Com



What Is The Formula Of Tan2x Quora



Trig Identities Hsn Forum




Prove Tan2x 2tanx 1 Tan 2 X Maths Introduction To Trigonometry Meritnation Com



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero




9 1 Identities And Proofs Ppt Download
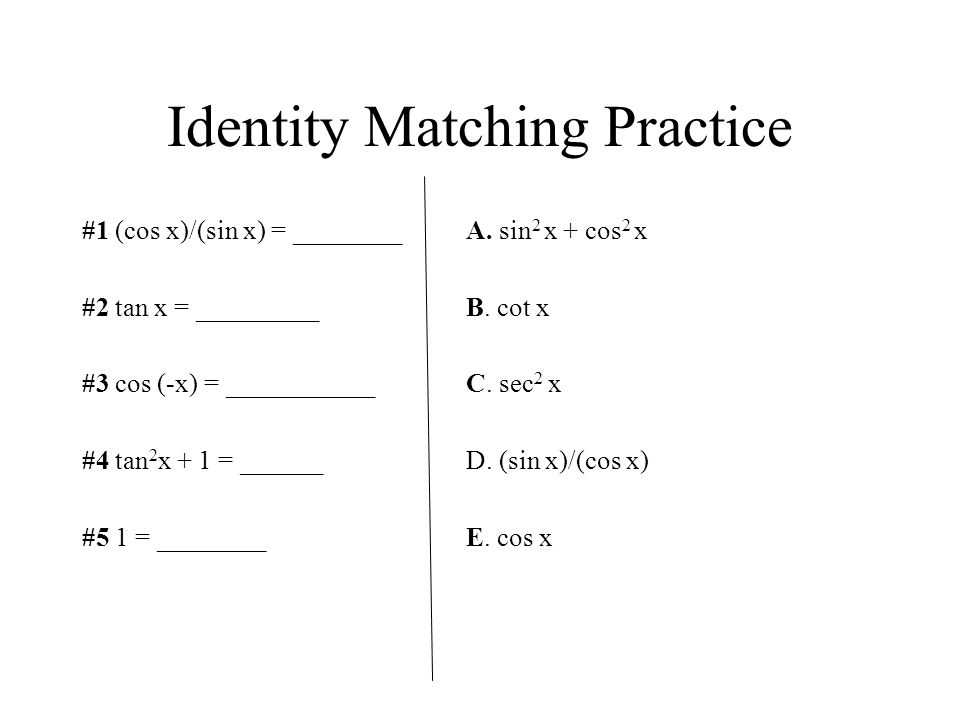



5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic




Double Angles Ppt Video Online Download
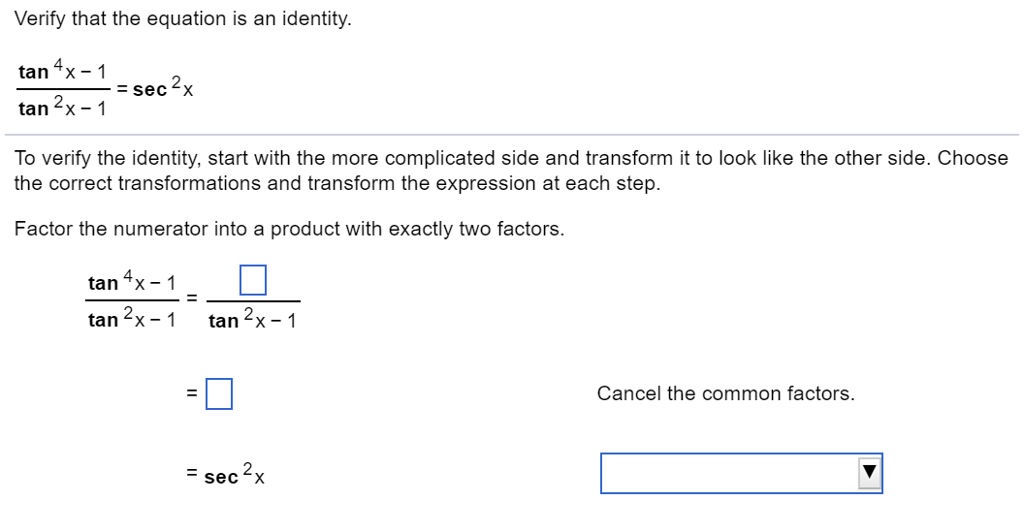



Verify That The Equation Is An Identity Tan 4x 1 Chegg Com


