両端固定 中心集中荷重 両端固定 偏芯集中荷重 両端固定 等分布荷重 両端固定 ← 図をクリックすると、 各種計算式が表示されます。 反力、せん断、曲げモーメント、 たわみ、・・・ Type はね出し単純 片側集中 はね出し単純 全体分布 両端固定 等分布 梁のたわみ計算式 両端固定梁で、ある点2箇所、1点は上から、もう1点は下からの集中荷重がかかる時の撓み計算式御存知の方いらっしゃいましたらご教授下さい。 │___↓_______│ ←この様な感じ │ ↑ │自由端:固定されていない端 ・両端支持はり ② 任意の点まわりに働くモーメントの和が0 である必要がある =150N 500mm 150mm 332 はりに生じるせん断と曲げモーメント (1) はりに作用する力のつり合い 集中荷重Wが支点Aからaの位置に作用している
両端固定梁のたわみ 応力 支持反力 集中荷重
両端固定梁 2点集中荷重 公式
両端固定梁 2点集中荷重 公式-集中荷重が作用する単純梁のたわみ=pl 3 /48eiです。 等分布荷重が作用する単純梁のたわみ=5wl 4 /384eiで求めます。 今回は両端支持のたわみ計算、公式、両端固定梁のたわみについて説明します。 また最大応力は固定端で生じ,その値σ は σ = M max Z = WL Z柱の座屈荷重の解法(2) 座屈応力に関する実験公式について解説する. 14 柱の座屈荷重の解法(3) 偏心や初期不整のある梁に軸圧縮荷重を作用させた場合の変形について解説する.また,短柱 座屈に関する実験公式を紹介する. 15 補遺:梁の曲げによる




はりの公式集 生産技術関連の情報ページ
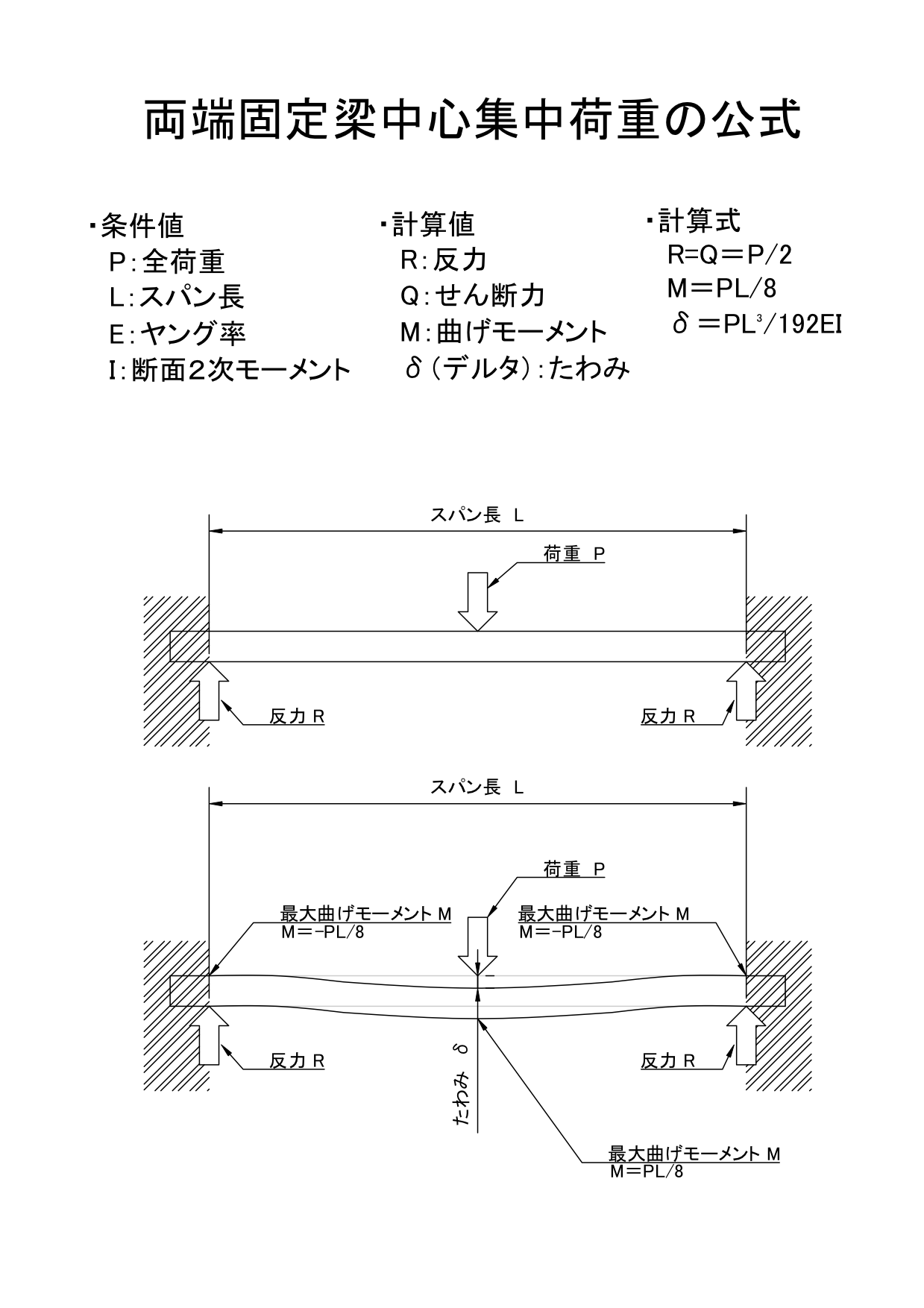
構造計算資料 梁公式集 1片持梁 2単純梁 3はね出し単純梁 41端ピン他固定 5両端固定梁 6連続梁 7三角形の面積 携帯用壁紙片持ち先端荷重 片持ち集中荷重 片持ち等分布荷重 両端支持中心荷重 両端支持任意等分布荷重 両端支持等分布荷重 両端固定中心荷重 両端固定任意等分布荷重 両端固定等分布荷重 両端支持 両端固定 δ = pl 3 3ei ≒ 45 δ = 800×500 3 3××1054×10 4単純梁と両端固定梁の公式 ・中心集中荷重 最大せん断力 単 純 梁:r=q=p/2 両端固定梁:r=q=p/2 最大曲げモーメント 単 純 梁:m=pl/4 両端固定梁:m=pl/8 最大たわみ 単 純 梁:δ=pl³/48ei 両端固定梁:δ=pl³/192ei ・等分布荷重 最大せん断力 単 純 梁:r=q=pa/2 両端固
荷重点の間では、仮想断面の左右の外力が変化しないので、せん断力は一定になります。 図のように両端支持梁に3つの集中が銃が作用すると、梁が4区間に分けられて4つのせん断力が発生します。 これらの4つのせん断力f 1 ・f 2 ・f 3 ・f 4 を求めなさい集中荷重を受ける片持ちばり 一端を固定し他端に横荷重 pを採用する梁のことを 片持ち梁といい1点に集中して作用する荷重のことを 集中荷重という。 8 は曲げモーメントの定義である。 可動・回転支点では、曲げモーメントはゼロですからね!2 6 等分布荷重と両端にモーメントが同時に作用 EI wl M M EI EI wl M M EI B A A A B 24 2 6 τ 24 2 6 τ 3 3 モーメントを求める式に変換 中間荷重が無 い場合と同じ 中間荷重が作用し た時の固定端モー メント 12 wl2 12 wl2 固定端:τA 、τA=0MAB=MBA= 12 wl2 12 2τ τ 2 12 2τ τ 2
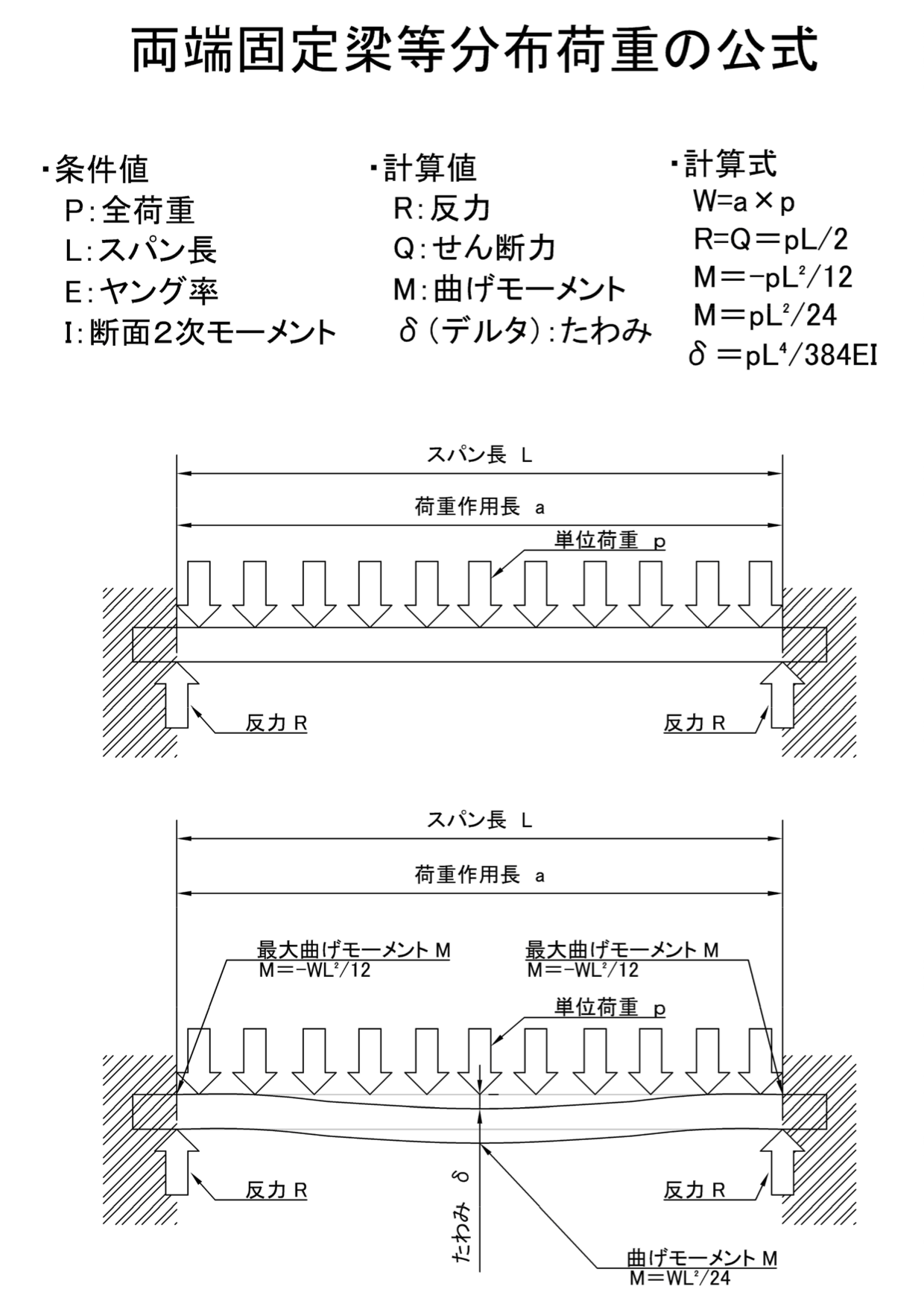
等分布荷重の梁は、M=wL 2 /8が公式です。 両端固定梁では、最大曲げ応力が変わります。 今回は両端支持はりの最大曲げ応力の求め方、公式について説明します。 複数の荷重が作用する、両端支持はりの最大曲げ応力は下記が参考になります。 最大曲げ・中央集中荷重 単純梁 ・等分布荷重 単純梁 ・先端集中荷重 片持ち梁 ・等分布荷重 片持ち梁 下図も重要な公式です。なお、両端固定梁の中央曲げはwL 2 /24です。 ・中央集中荷重 両端固定 ・等分布荷重 両端固定 ・中央集中荷重 片側ピン片側固定 2 6 等分布荷重と両端にモーメントが同時に作用 EI wl M M EI EI wl M M EI B A A A B 24 2 6 τ 24 2 6 τ 3 3 モーメントを求める式に変換 中間荷重が無 い場合と同じ 中間荷重が作用し た時の固定端モー メント 12 wl2 12 wl2 固定端:τA 、τA=0MAB=MBA= 12 wl2 12 2τ τ 2 12 2τ τ 2構造計算 – 両端固定梁 試作のお



単純梁に集中荷重が2箇所にかかっている場合のたわみの算出方法を教えてく Yahoo 知恵袋




2点集中荷重片持ち梁について 2点集中荷重片持ち梁の曲げモーメントと 数学 教えて Goo
Q&A一覧 公式・専門家 質問・相談 「両端固定梁」の検索結果 質問一覧 画像の等分布荷重を受ける両端固定梁のA点及びB点に生じるモーメントの求め方を教えて欲しいです。 答え 答えは Ma = wol^2/12 Mb = wol^2/12 になるそうです。 分かる方よろしくお願い11 例題1集中荷重を受ける両端単純支持はり 図1 に示すはりのsfd、bmd を求めなさい。 p r1 l r2 1 a b c l 2 l 図1 集中荷重を受ける両端単純支持はり 解 点c で仮想的に分割すると、図2 の下のようになります。 p r1 l r2 1 a b c l2 r1 r2 r1 r2 図2 点c で分割 反力r1 とr25 片持ち梁のたわみとたわみ角 51 ③片持ち梁の




片持ち梁に2個の集中荷重が作用するとき 添付図のような片持ち梁があります Okwave



2点集中荷重が作用する両端固定梁の公式は 1分でわかる求め方 解き方 と計算
梁のたわみと応力計算ツール 利用方法 Step1:梁の種類を選択 Step2:断面の種類を選択 Step3:材料を選択 Step4:各数値を入力 計算を実行すると、梁のたわみ量 (mm)、応力 (MPa)、重量 (kgf)が出力されます。 Step1 梁の支持方法を選択します。 片持ち直荷重Pが作用した場合、A、C点の鉛直反力の絶対値として、正 しいものは次のうちどれか。ただし、梁は等質等断面とする。(H5) 2l0 2 40l p a c b 過去問56 同じ単純梁が等分布荷重wおよび集中荷重Pを受け る場合の梁の中央の鉛直変位が ei wl a 384 5 4 g図632 b点を剛体壁とする2つの片持ちはり 変形後の状態を図633に示す。 図633 変形後の状態 すなわち,集中荷重r1によりa点はa'点に移動しそのたわみ量を 1 , r2 によりc点はc'点に移動しそのたわみ量を 2とすると,教



曲げモーメントの公式は 1分でわかる公式 導出 両端固定 単純梁 片持ち梁
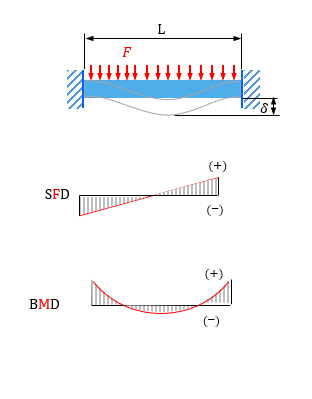



梁のたわみと応力計算ツール
単純梁で梁の中央への集中荷重の曲げモーメントの公式が M=PL/4となる理由(公式にいたる過程の式)を教えてください。 いろいろなサイトを見ましたが、公式は載っていてもなぜそうなるのかを説明している サイトがみつかりませんでした。 片持はりに集中荷重が作用する場合のたわみの公式 長さsの片持はりの自由端に、集中荷重Pが作用する場合のたわみの公式は、以下のとおり。 固定端Aでたわみは0、自由端Bでたわみは最大となります。 y(x) = P(x 3 – 3xs 2 x 2s 3)/6EI y max = Ps 3 /3EI梁の公式 荷重・形状 条件 曲げモーメント m反力 r・せん断力 q・全荷重 w たわみ δ P l ab c Ra Rb 2 ra=rb= w=p p 2 p mc= δc= 48ei pl3 P l c Ra Rb ab w=p ra=qa= pb rb=-qb= pa mc= δc= pab 3eil 2 2 P l c Ra Rb P c l/3 l/3 l/3 ra=rb=p qa=-qb=p w=2p 3 pl =mmax



単純梁の曲げモーメントは 1分でわかる求め方 計算 公式 等分布荷重と集中荷重との関係
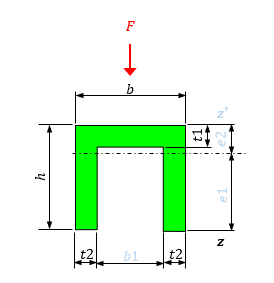



梁のたわみと応力計算ツール
例題52次の単純ばりの反力を求め,Q図,M図を描け. 解 1) 反力 A 荷重は分布荷重のままでは扱いにくいので,その重心 に作用する集中荷重に置き換えて考える.すなわち, 図 l/2 の点に ql (kN)が作用していると考える. 左右対称であるから M 2 ql R A R B .図 81(a)には、梁が曲げ変形を生じる前の状態が示されており、最初 に、原点より xの位置に微少な間隔 dxの両端に材軸に垂直な2つの平 面を考える。これを法面と呼ぶ。次に、荷重を受け、材が曲がった後の 変形状態を考え、断面内のひずみと応力を求める。図のように剛体壁で両端を固定されている直径d 1 と直径d 2 の丸棒の場合に温度をΔT上昇させた場合に次の値を求める。 Eは弾性係数、αは線膨張係数である。 ・自由熱膨張の場合に、各材料の伸び、δ 1,δ 2 を求める。 ・C点の移動距離δ c を求める。




たわみ計算 2点集中荷重 両端支持梁 A Okwave
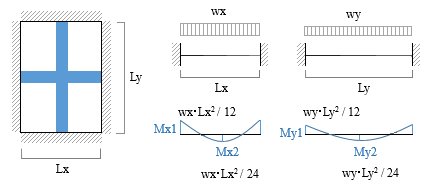



電卓で構造計算 スラブ編
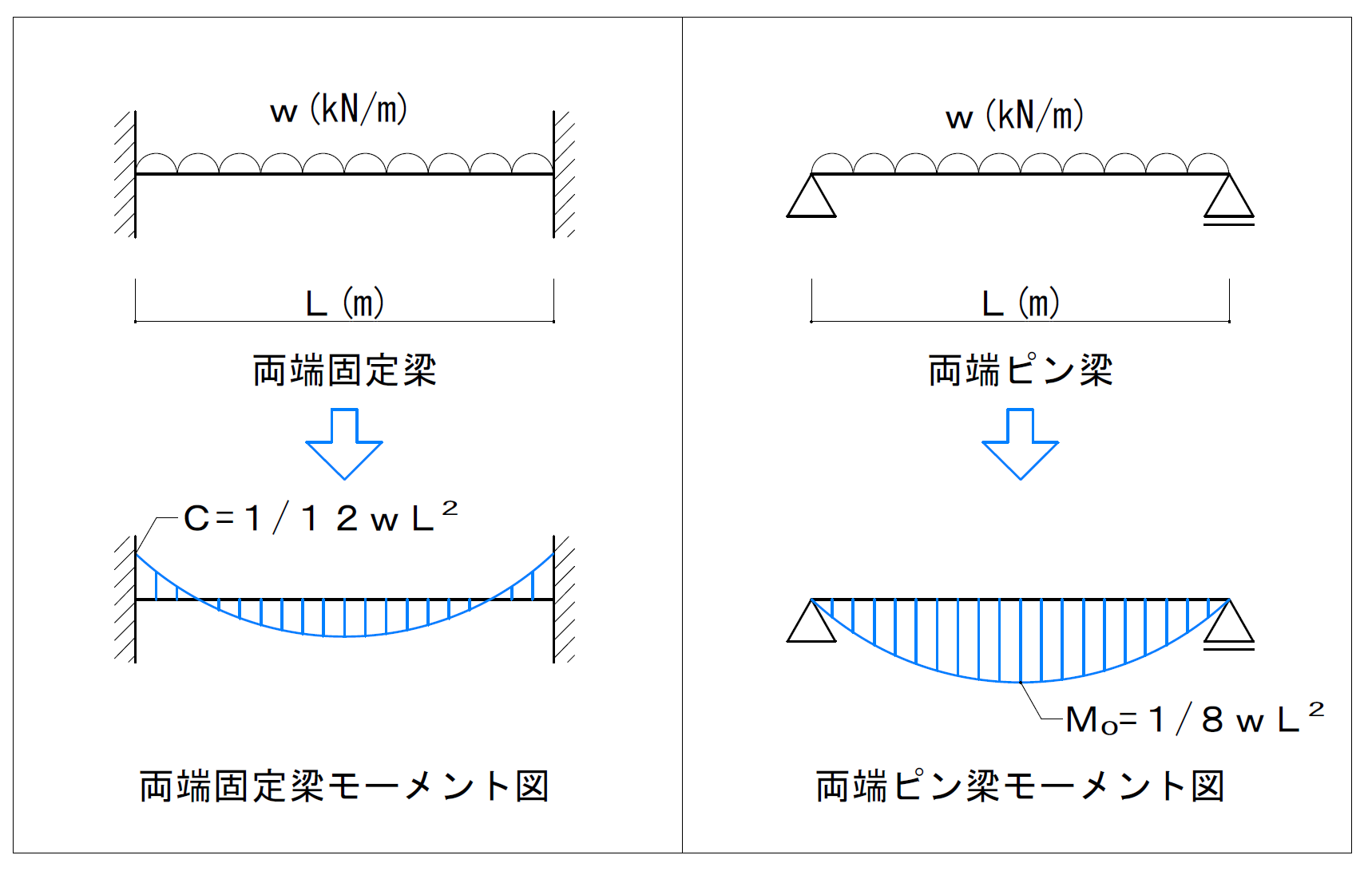
C116 講義資料 材料力学 Golden, CO, USA (09) 京都大学農学部地域環境工学科 中嶋 洋 Ver 41 ①単純梁の集中荷重・・・これが、基本っ! 411 覚えておくポイントその1;両端固定梁及び単純梁モーメント 基本的な両端固定梁モーメント 基本的な両端固定梁の等分布荷重と集中荷重のモーメントを求める公式は次のようになります。 等分布荷重時 両端M=(1/12)wl 2 中



どなたかご教授下さい 2点集中荷重の両端支持はりの指定箇所にかか Yahoo 知恵袋



やさしい実践 機械設計講座
法を学ぶ。下図に示す部材中央に集中荷重が加わる両端固定梁を解析モ デルとし、部材の変形状態、載荷点の鉛直変位、曲げモーメント分布な どを求める。 x 図111 両端固定梁の解析モデル 変位と荷重には以下のような関係がある。 4 4 zw() dw EI P x dx =Ⅰ 構造力学(解法2) 構造力学を習得する上で必要な基礎的な考え方は〈構造力学(法則・基本的な考え方)〉で紹介し,解法の与条件は〈構造力学(解法1)〉で紹介しました。 次は,その考え方を使って構造問題をどうやって解くかです。•両端の支点では、固定支点でなければ支点 モーメントは作用しない。 𝑀1=𝑀 =0 この2つの式と中間の支点に作用するk-2個の支 点モーメントを持ち数として3モーメントの式を立て れば、𝑀2,⋯,𝑀 −1を求める
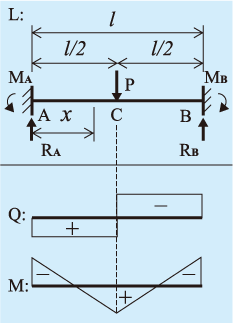



構造計算 両端固定梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社



2点集中荷重が作用する両端固定梁の公式は 1分でわかる求め方 解き方 と計算
42 ②単純梁の等分布荷重 421 覚えておくポイントその2; 固定端bに強制変位Δを受ける不静定はりについて、たわみとたわみ角の関数を求めよ。 但し、曲げ剛性をEIとし、これを一定の物 とする。 解決済み 質問日時: 008 回答数: 1 閲覧数: 338静定はりと不静定はり 静定はり 未知変数、反力、固着モーメント 力のつりあい A点周り 支点A、Bの2か所で支持されている単純両支持の梁に支点Aから距離xの位置に 集中荷重がある時、この梁の最大曲げ荷重のかかる位置はxの位置で良いでしょうか? 計算方法の正誤を知りたいので、いくらか条件説明は省略させて頂きますが、 まず、支点A,B



両端固定梁とは 梁の両端を接合 機械卒でも土木の現場監督



許容応力度とたわみによる断面算定の考え方 県木連のホームページ 一般社団法人愛知県木材組合連合会
33 両端固定梁 ・・・・・・・・・・・・・・・ 10 4.断面性能 31 片持ち梁 梁に曲げ荷重をかけると、梁内部には、引張応力、圧縮応力及びせん断応力が発生し 本項では、両端支持梁の曲げ変形の公式を示します。2方向に比べ大. 横方向の力. 柱:長さが他の 2 方向に比べ大. 長さ方向の圧縮力. 梁ー柱:長さが他の 2方向に 比べ大.両方向の力. 曲がり梁 ケーブル 二次元 板:厚さに比べ 他の 2 方向の寸法が大. 殻 三次元 固体 10両端固定梁 梁の中間に集中荷重 xbの時 x=aでは x=aでは xaの時 xaの時 ではもし ならば では もし ならば 中心では 中心では 中心では 両端 支持 梁 任意の位置にモーメント付加 の時



両端固定梁とは 梁の両端を接合 機械卒でも土木の現場監督




両端支持梁に集中荷重 2か所 の場合の最大応力 Okwave
集中荷重を足し・・・引くんだっけ・・・ん? う面ではどうなのか,門外漢の著者には見当がつかないので,この点については読者の 2 = 0 を導く.これを使って12 章では,第i 部で天下りに与えた両端支持のたわみ計算は、荷重条件と支持条件で変わります。集中荷重が作用する単純梁のたわみ=pl 3 /48eiです。 等分布荷重が作用する単純梁のたわみ=5wl 4 /384eiで求めます。 今回は両端支持のたわみ計算、公式、両端固定梁のたわみについて説明します。 両端固定 等分布荷重 モーメント梁のたわみと応力計算ツール 利用方法 Step1:梁の種類を選択 Step2:断面の種類を選択 Step3:材料を選択 Step4:各数値を入力 計算を実行すると、梁のたわみ量 (mm)、応力 (MPa)、重量 (kgf)が出力されます。 Step1 梁の支持方法を



肩持ち梁のせん断力計算問題 集中荷重が複数の場合 建築学科のための材料力学



小梁の設計 C M Qとは 構造設計memo



両端固定梁のたわみ 応力 支持反力 集中荷重



両端固定梁のたわみ 応力 支持反力 集中荷重
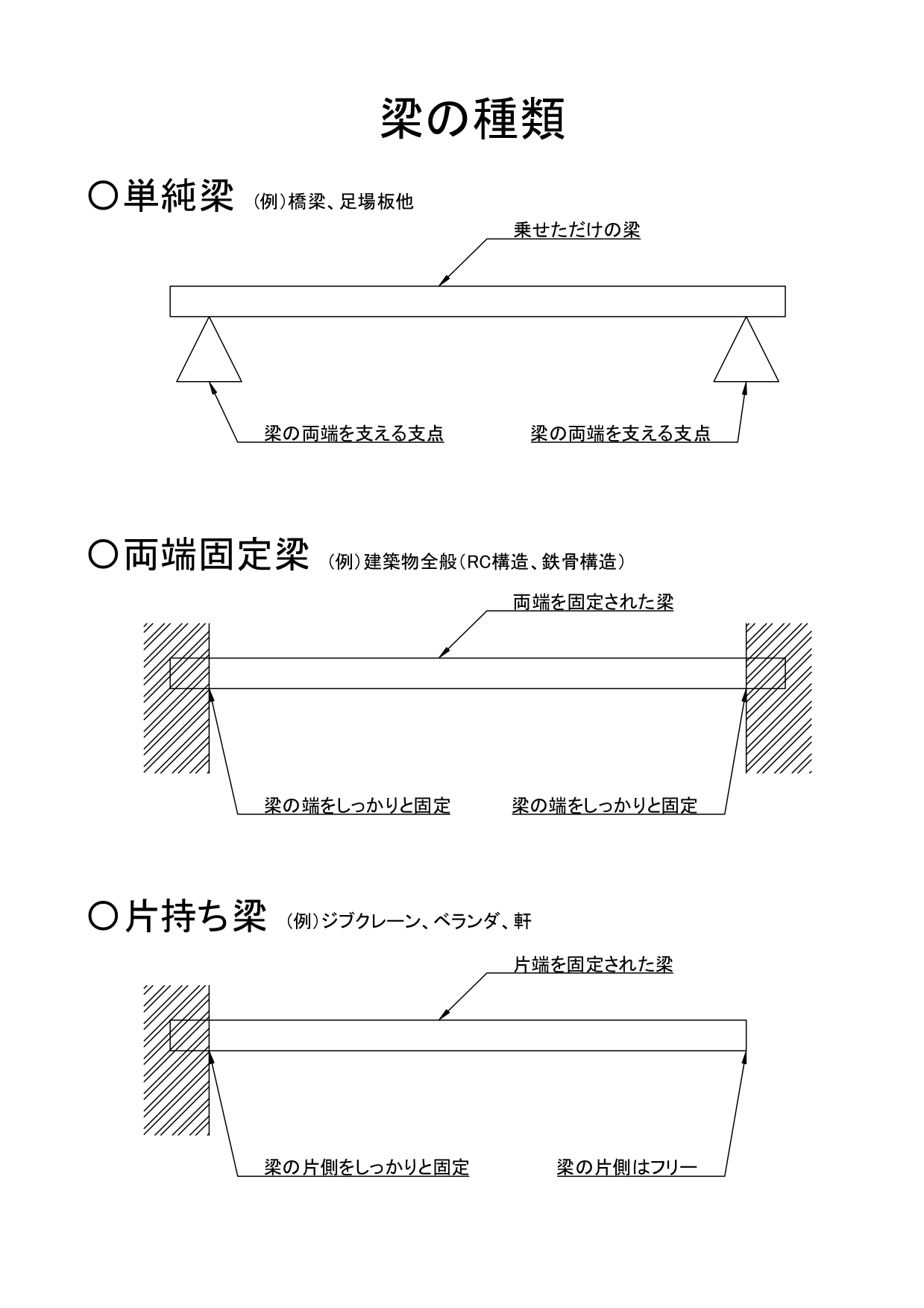



両端固定梁とは 梁の両端を接合 機械卒でも土木の現場監督



両端支持梁のせん断力計算問題 複数の集中荷重を受ける場合 建築学科のための材料力学



両端支持はりの計算 はりのたわみ計算 オンライン



片持ちはりのたわみ計算 はりのたわみ計算 オンライン




はりの公式集 生産技術関連の情報ページ
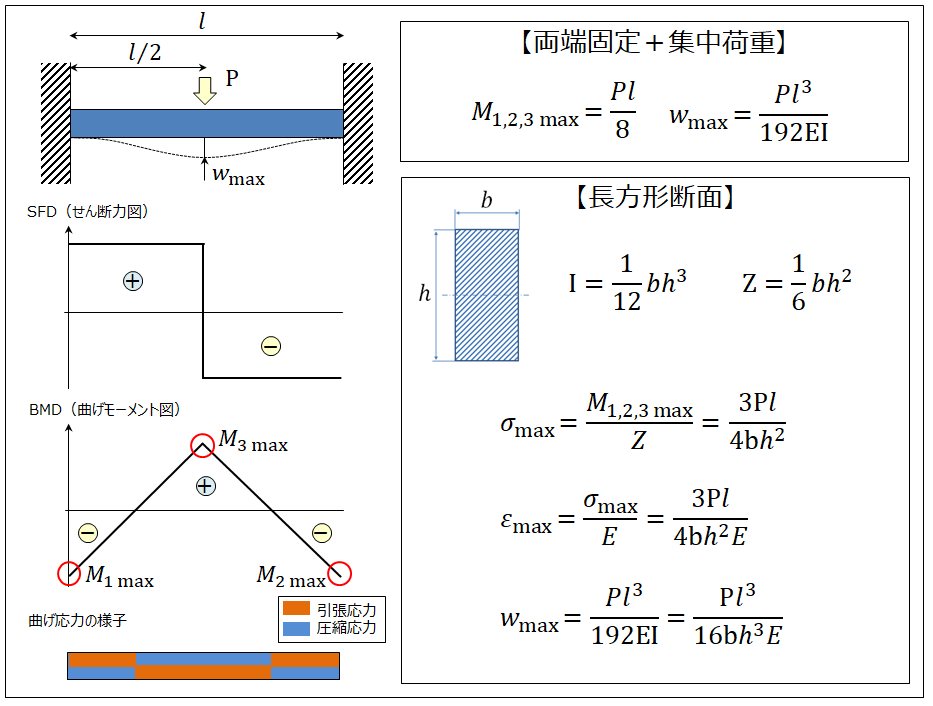



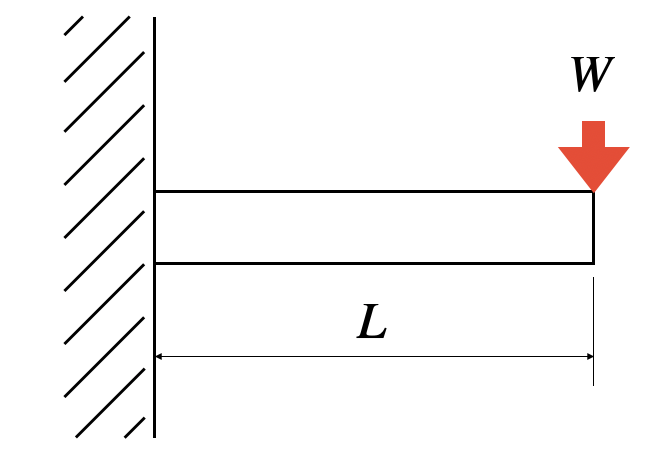
はりの強度計算 両端固定 集中荷重 長方形 製品設計知識




一級建築士試験で覚えておくたわみとたわみ角の覚え方 建築士試験の勉強法




両端固定はりのせん断力と曲げモーメント 図のような固定はりのせん断力 曲 Okwave



Www Jp Omega Com Techref Pressure43 67 Pdf



たわみとたわみ角の覚えるべき公式と過去問解説 一級建築士の構造 一級建築士への道



両端支持梁の支点反力を求める例題を紹介 建築学科のための材料力学



棚板の耐荷重の考え方と 耐荷重計算のやり方を解説します とある建築士の憂鬱



コンサルhiroの構造解析入門講座 梁の公式2 曲げモーメントによる梁内の応力と梁のたわみ



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ



単純梁の曲げモーメントは 1分でわかる求め方 計算 公式 等分布荷重と集中荷重との関係




集中荷重が掛かる片持ちハリの曲がる形は f 物理学 教えて Goo



曲げモーメントの公式は 1分でわかる公式 導出 両端固定 単純梁 片持ち梁



図に示すような2つの集中荷重 P1 600n P2 10nをうけるハリの半 Yahoo 知恵袋



Excel 123 Stress ビギナーズ向け構造計算



第8章 構造解析法への適用



梁 反力 曲げモーメント たわみ 曲げ応力 公式集 計算ツール ものづくりのススメ
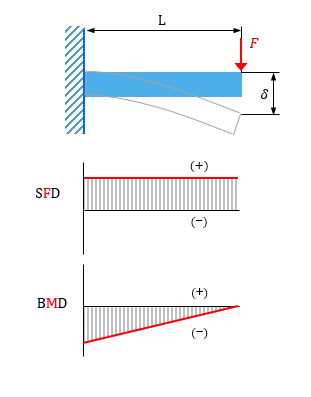



梁のたわみと応力計算ツール
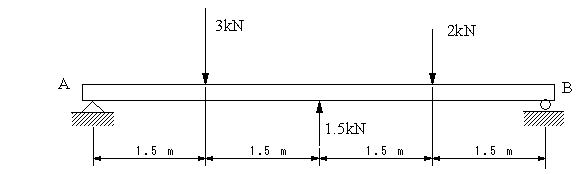



材料力学の典型的な問題



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ



単純梁に集中荷重が2箇所にかかっている場合のたわみの算出方法を教えてく Yahoo 知恵袋
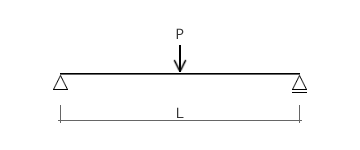



Dansan 公式



両端固定梁のたわみ 応力 支持反力 集中荷重



はりの話 後編




はりのひずみの計算式 共和電業
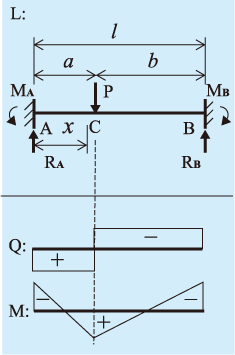



構造計算 両端固定梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社
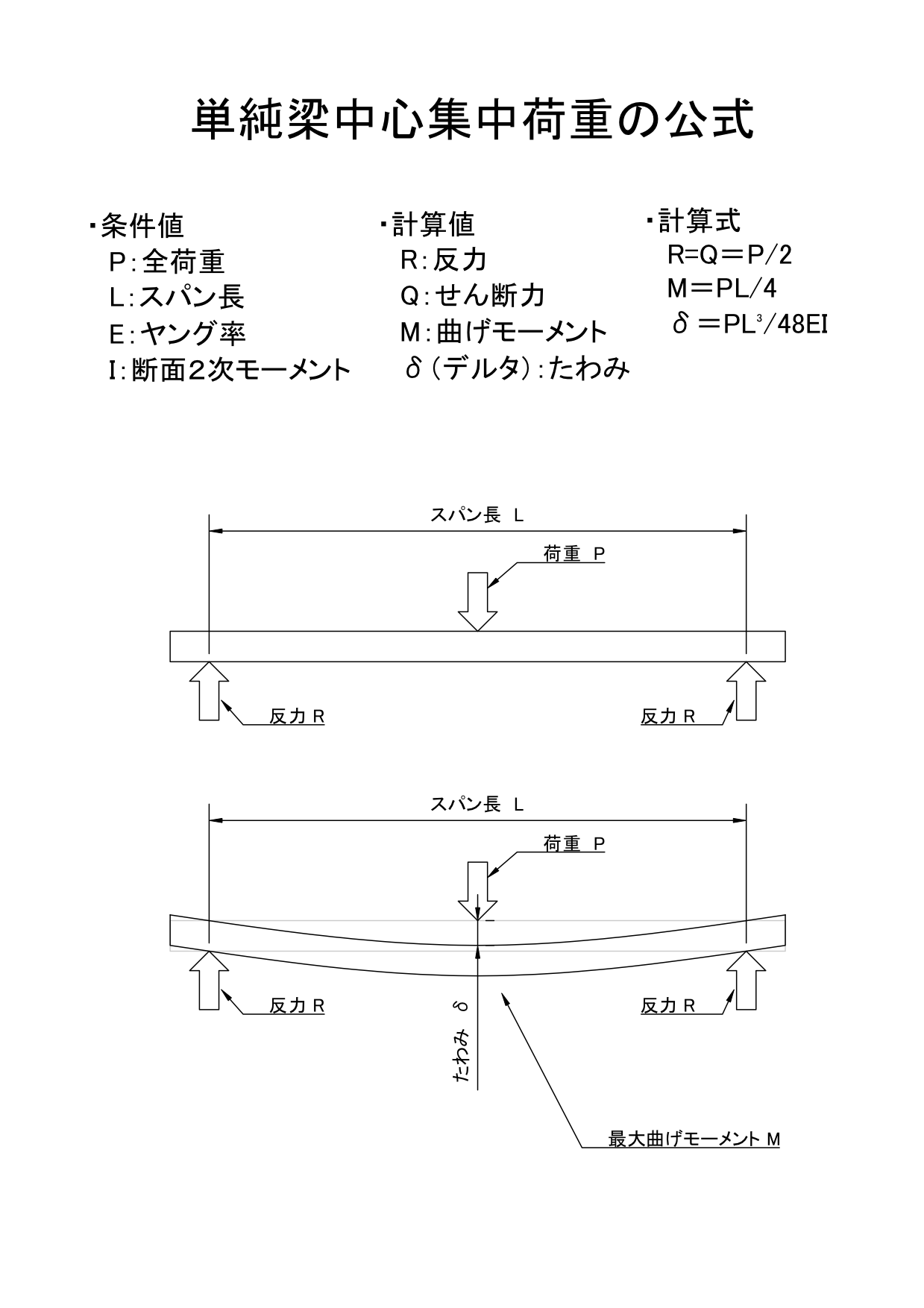



単純梁とは 梁を置いただけ 機械卒でも土木の現場監督
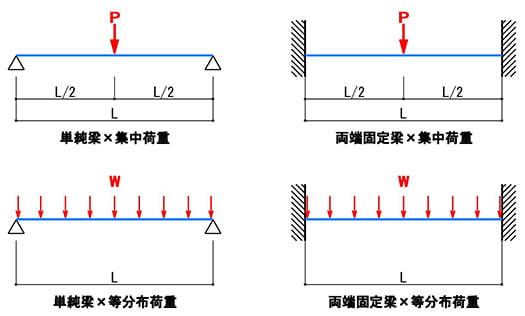



棚板の耐荷重の考え方と 耐荷重計算のやり方を解説します とある建築士の憂鬱



梁 反力 曲げモーメント たわみ 曲げ応力 公式集 計算ツール ものづくりのススメ



曲げモーメント せん断力 たわみの計算式 県木連のホームページ 一般社団法人愛知県木材組合連合会



両端支持梁の曲げモーメントの求め方は 計算方法について 建築学科のための材料力学



両端固定はりのたわみ計算 はりのたわみ計算 オンライン




2点集中荷重の計算について教えてください 2点集中荷重の計算につ 物理学 教えて Goo




2点集中荷重片持ち梁について 2点集中荷重片持ち梁の曲げモーメントとたわ Okwave
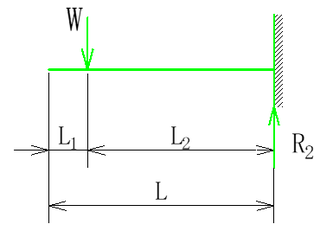



はりの公式集 生産技術関連の情報ページ




3点集中荷重の最大曲げ応力の計算式を教えてください 足場架設用の仮 物理学 教えて Goo



2点集中荷重が作用する両端固定梁の公式は 1分でわかる求め方 解き方 と計算



単純梁の計算公式 対称2点集中荷重




両端支持梁に集中荷重 2か所 の場合の最大応力 両端支持の梁に2か所 物理学 教えて Goo
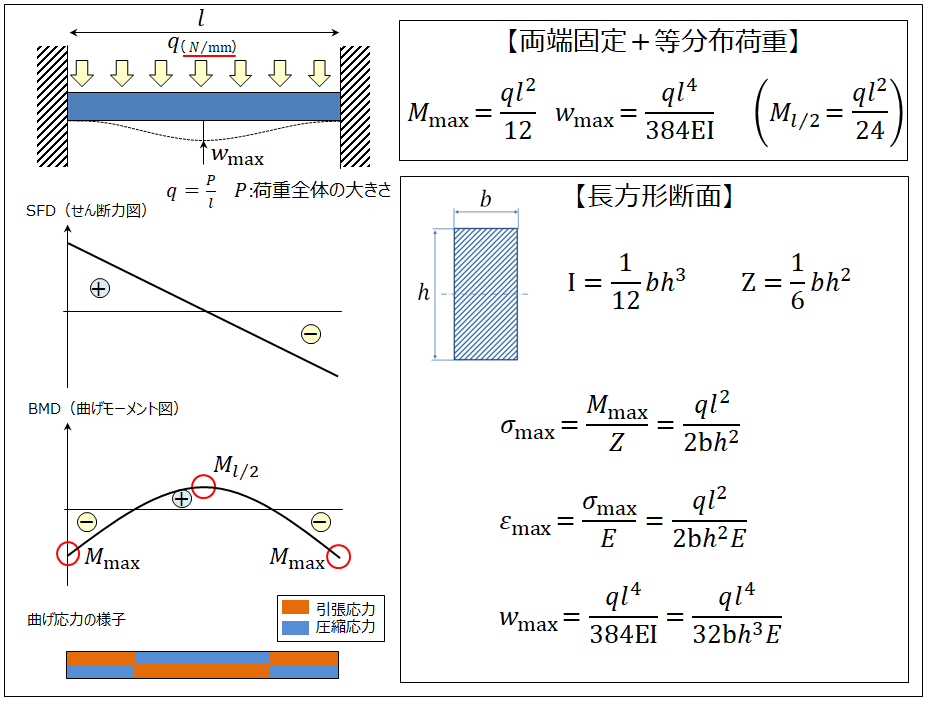



はりの強度計算 両端固定ー等分布荷重ー長方形 製品設計知識
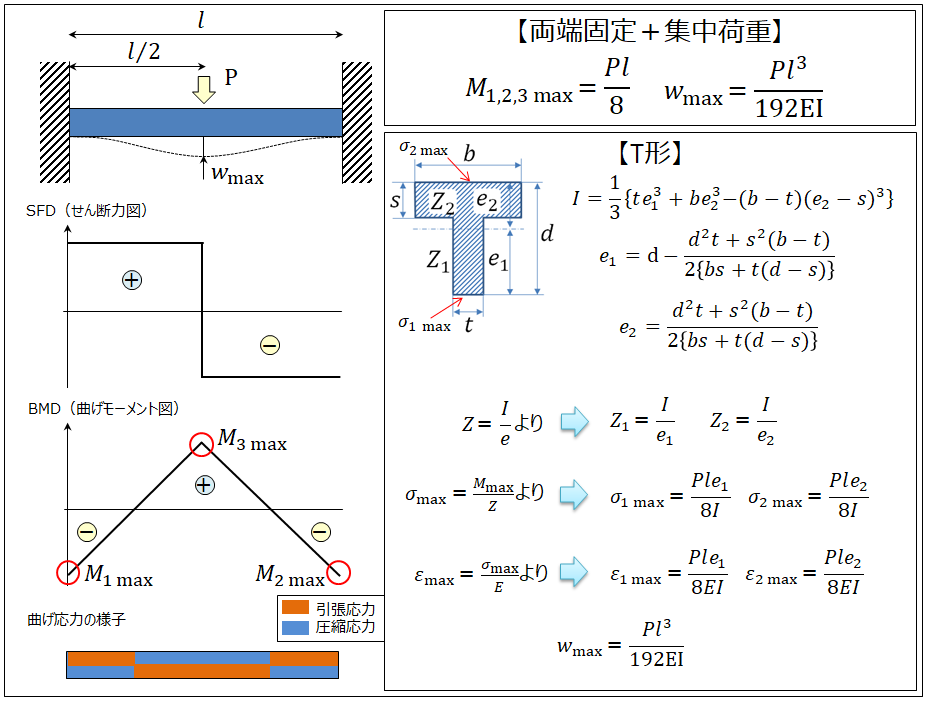



はりの強度計算 両端固定ー集中荷重ーt形 製品設計知識



棚板の耐荷重の考え方と 耐荷重計算のやり方を解説します とある建築士の憂鬱
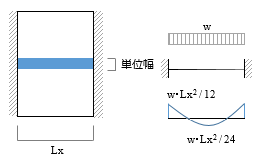



電卓で構造計算 スラブ編



曲げモーメント せん断力 たわみの計算式 県木連のホームページ 一般社団法人愛知県木材組合連合会
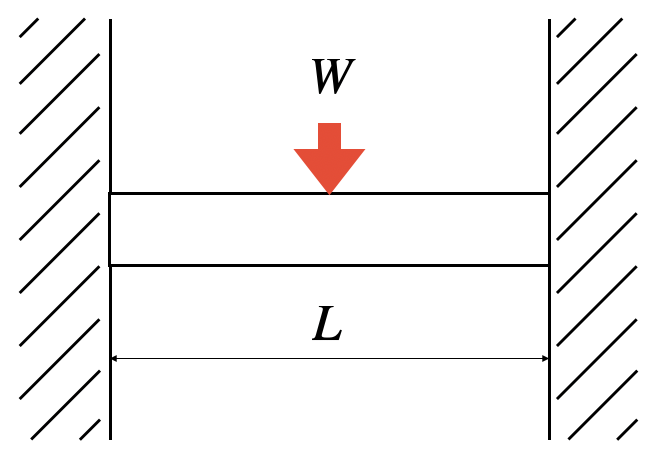



梁 反力 曲げモーメント たわみ 曲げ応力 公式集 計算ツール ものづくりのススメ
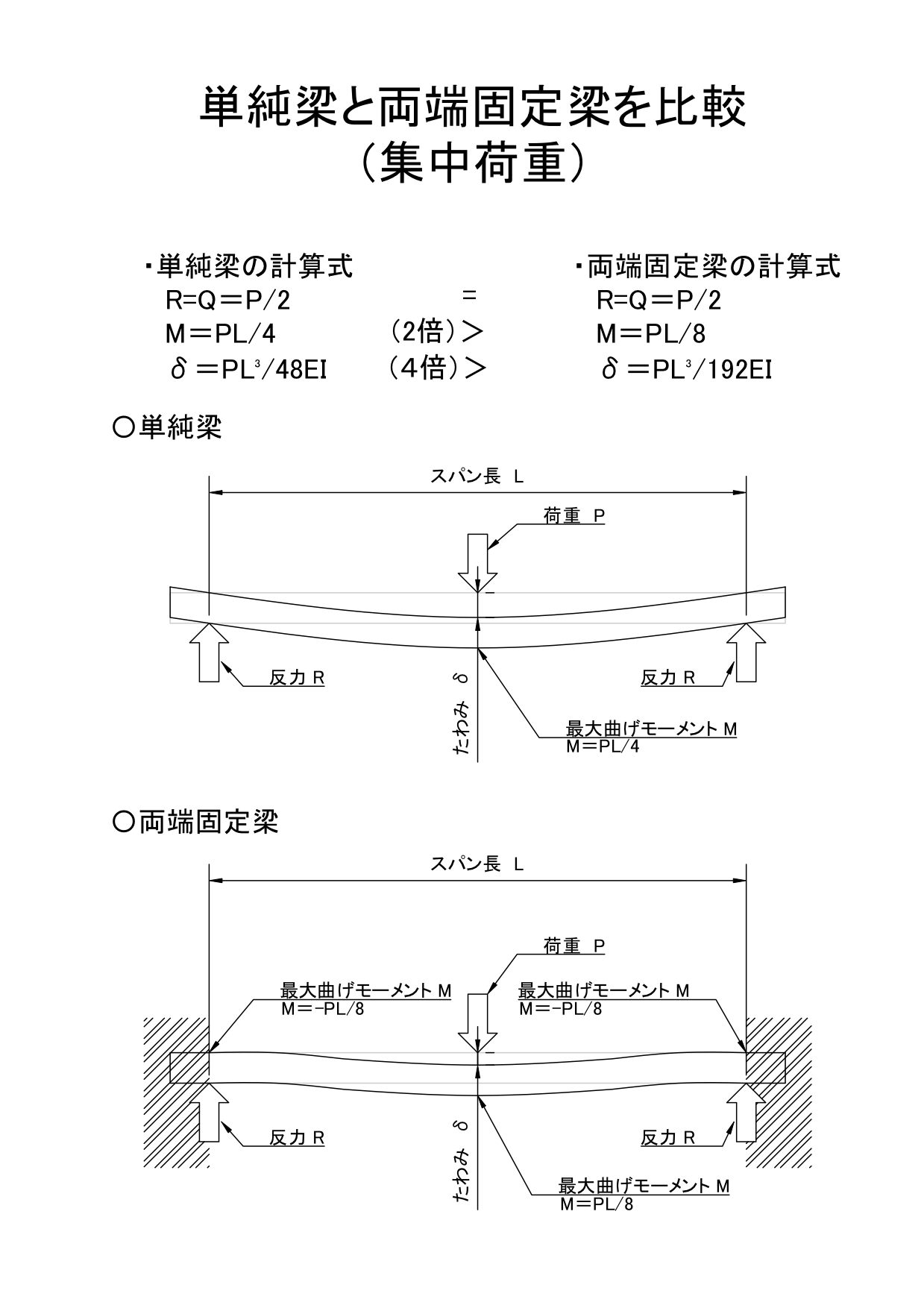



単純梁と両端固定梁を比較 単純梁の方が変位が大きい 機械卒でも土木の現場監督
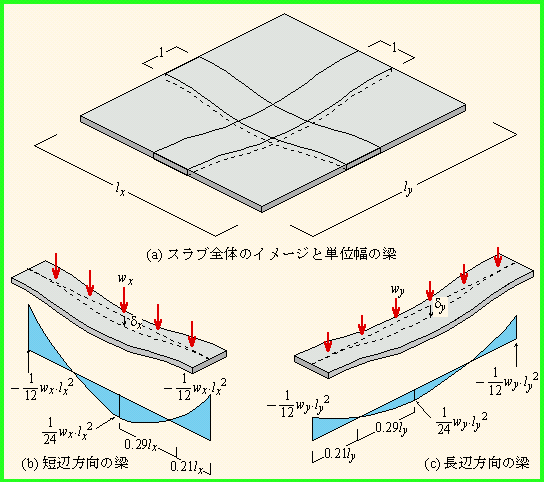



8 2 周辺固定スラブ



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ
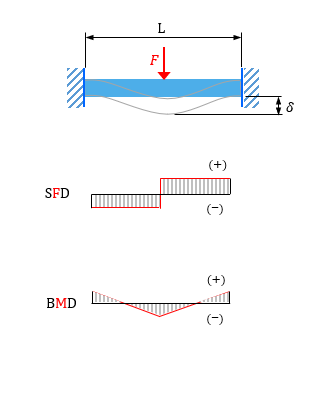



梁のたわみと応力計算ツール



梁 反力 曲げモーメント たわみ 曲げ応力 公式集 計算ツール ものづくりのススメ




久々の構造力学 一級建築士memo



梁 反力 曲げモーメント たわみ 曲げ応力 公式集 計算ツール ものづくりのススメ



はりの曲げモーメントせん断力解説
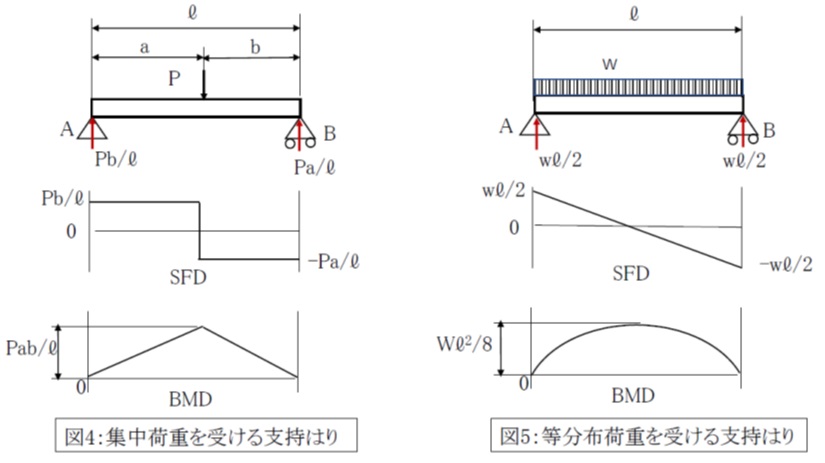



機械設計マスターへの道 はり の基礎知識を習得 Sfdとbmd たわみの計算方法は アイアール技術者教育研究所 製造業エンジニア 研究開発者のための研修 教育ソリューション



両端固定の梁に任意の位置に集中荷重がかかる場合の 任意の位置のたわみの公式が Yahoo 知恵袋



はりの話 前編



等分布荷重の計算と公式は 1分でわかる公式 計算方法 反力の求め方



コンサルhiroの構造解析入門講座 材料力学
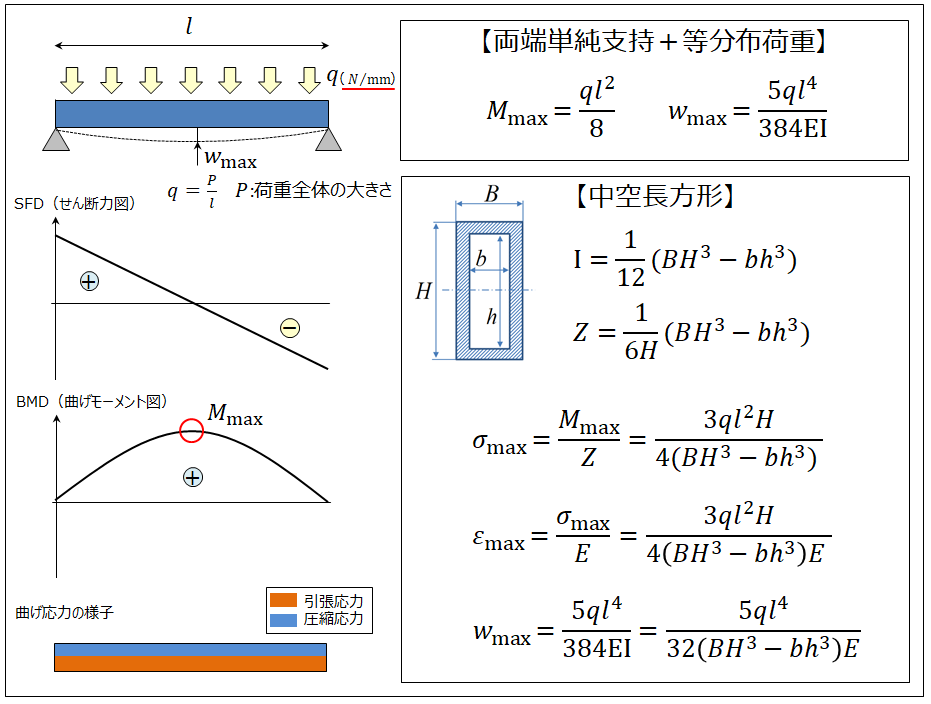



はりの強度計算 両端単純支持 等分布荷重 中空長方形 角パイプ
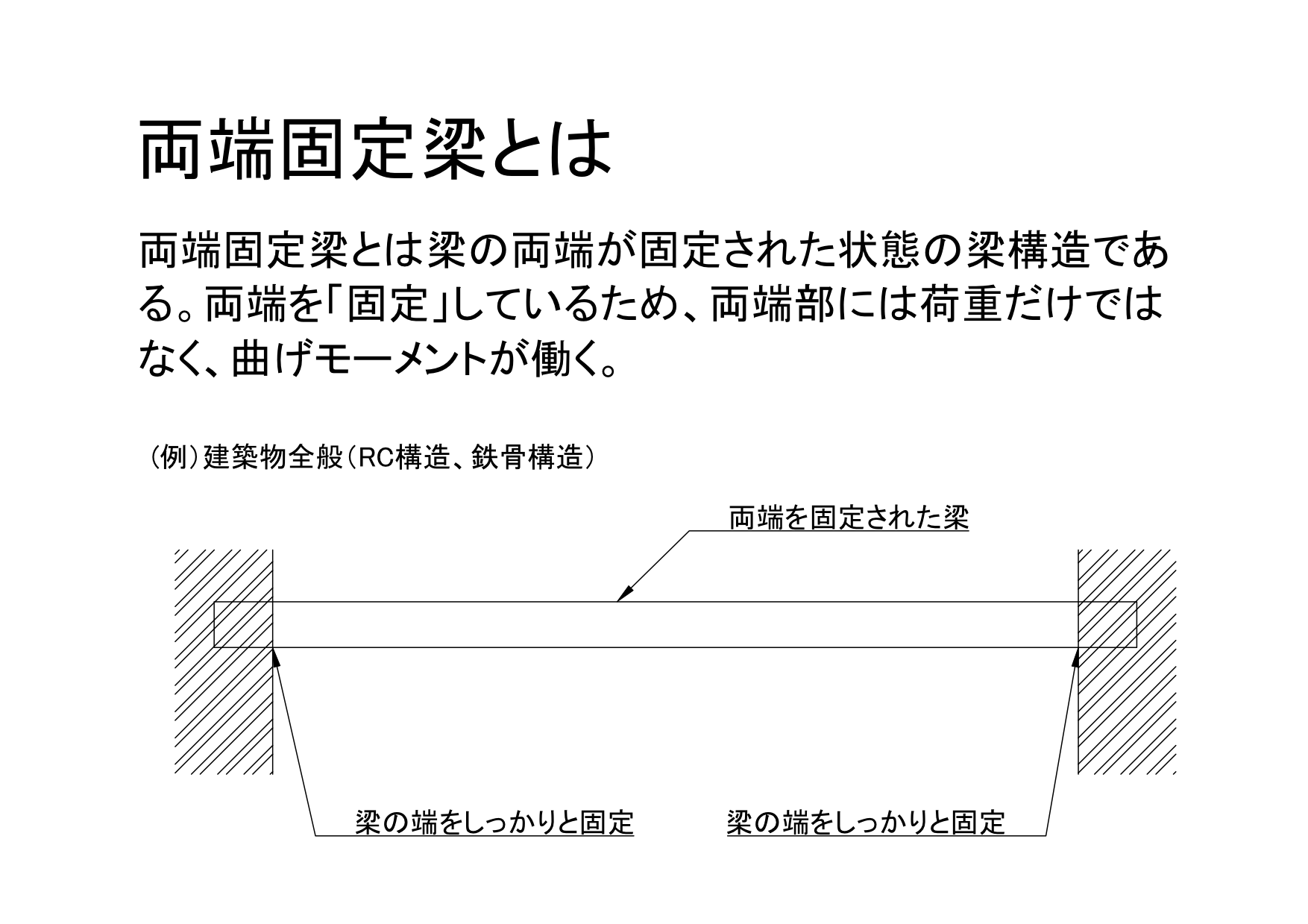



両端固定梁とは 梁の両端を接合 機械卒でも土木の現場監督



種々のはりのたわみ



Be3



2点集中荷重が作用する単純梁とは 1分でわかる意味 公式 たわみ 曲げモーメント



両端支持のたわみ計算は 1分でわかる計算 公式 両端固定梁のたわみ



両端支持はりの最大曲げ応力は 1分でわかる求め方 公式
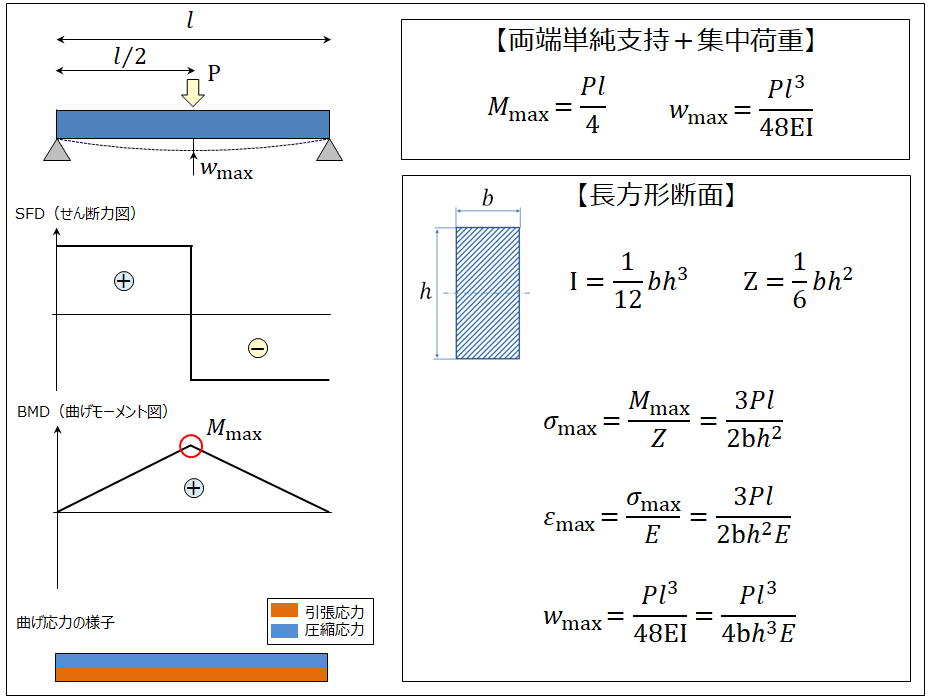



はりの強度計算 両端単純支持 集中荷重 長方形 製品設計知識
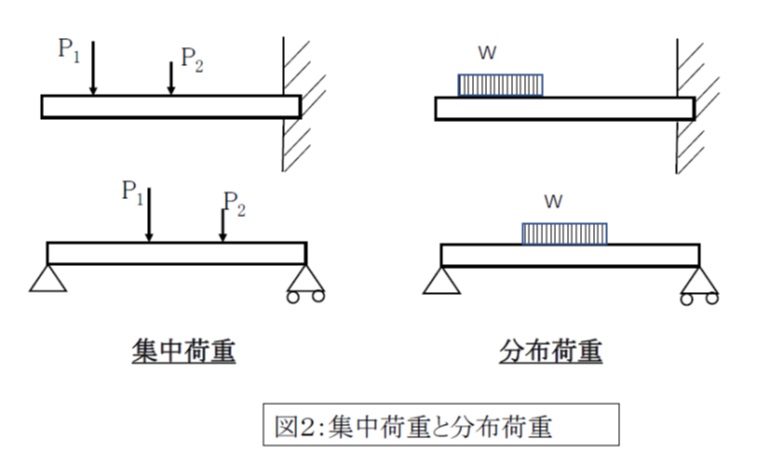



機械設計マスターへの道 はり の基礎知識を習得 Sfdとbmd たわみの計算方法は アイアール技術者教育研究所 製造業エンジニア 研究開発者のための研修 教育ソリューション




モールの定理 集中荷重編 たわみの公式を忘れても求められる とある若手構造設計者の徒然blog
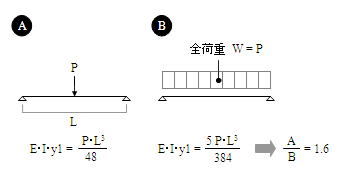



梁のたわみ量の計算について




たわみ計算 2点集中荷重 両端支持梁 A 物理学 教えて Goo
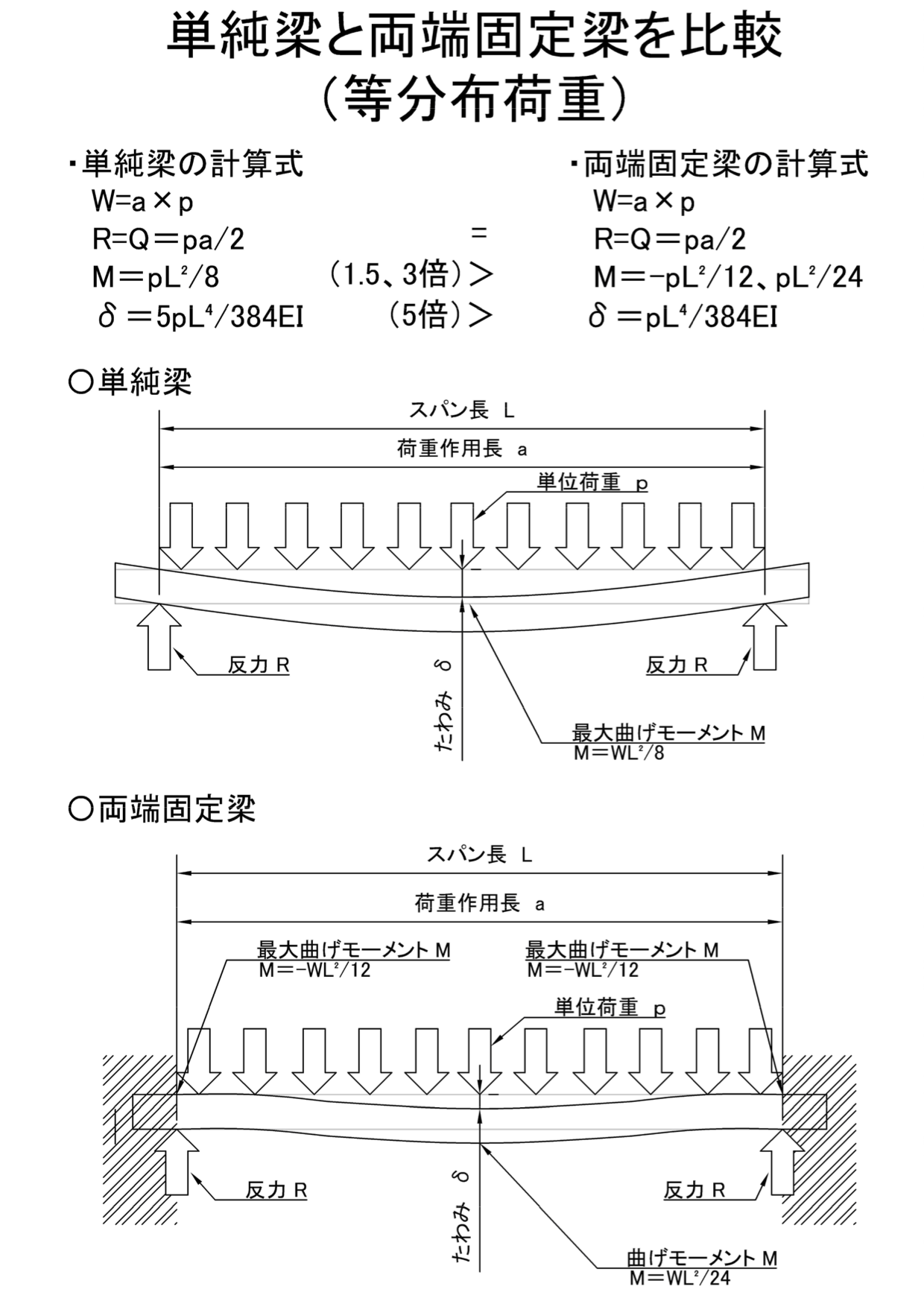



単純梁と両端固定梁を比較 単純梁の方が変位が大きい 機械卒でも土木の現場監督




02 はりの曲げ 集中荷重が作用するとき 材料力学の事前 事後学習課題作成のヒント



材料力学 梁のたわみに関しての質問です 両端固定梁 2点集中荷重はりの最大た Yahoo 知恵袋



2点集中荷重が作用する両端固定梁の公式は 1分でわかる求め方 解き方 と計算


